写在前面:
从这里开始,我们将一步步的学习、认知、掌握基础的算法规则。受限于自身的专业水平,文中提及的算法与实例代码多有优化的空间,但仍不失为一种可供学习参考的资料。
算法系列的文章源代码将陆续更新到github上,其地址如下:
https://github.com/zhaolingxi/AlgorithTtraining
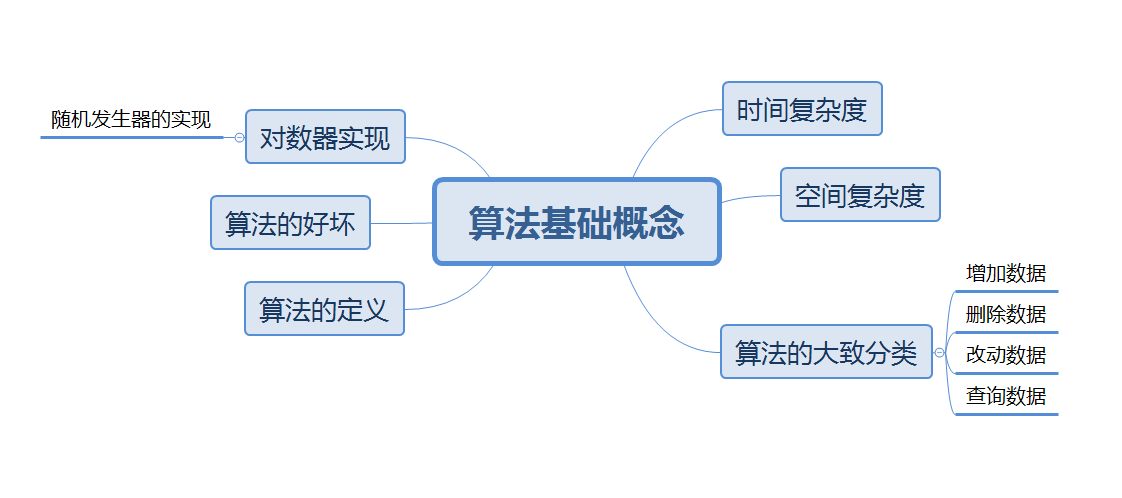
本系列将探讨的问题大致分为以下内容:
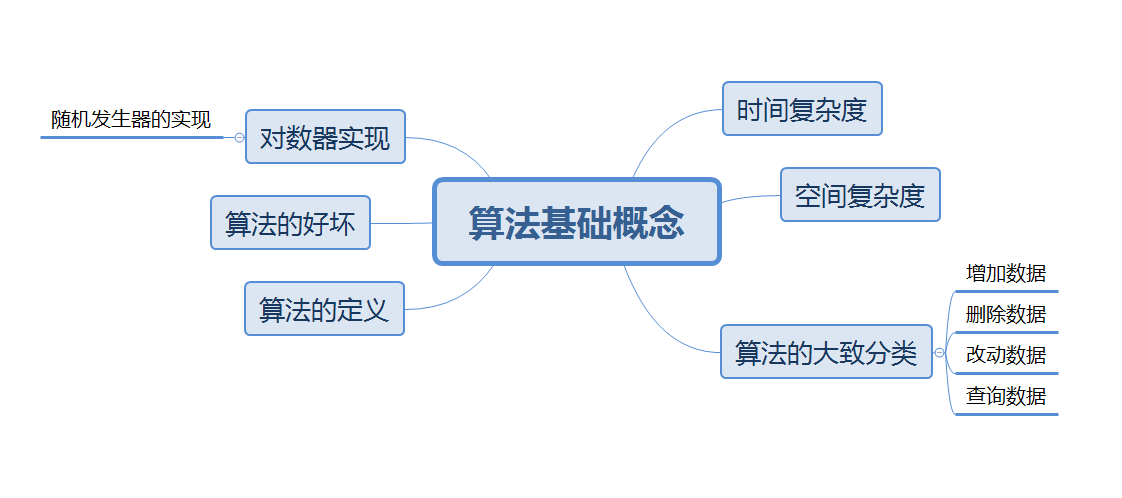
算法的定义:
这里我们指代狭义的计算机学科算法,其定义就是处理数据,并将处理数据的过程归纳集合起来,成为一种方法。
它有以下几个特点:
有输入:必须有0个或多个输入
有输出:有一个或多个输出,输出的量是算法计算的结果
确定性:每一步都应确切地、无歧义地。
有穷性:执行步数有限
可行性:每一条运算都必须是足够基本的。能通过计算机指令精确地执行,有限次计算就能完成
算法的作用:
用于处理计算机内部的数据
算法复杂度:
算法既然是处理数据与信息的方法,那执行这一个方法必然需要时间,同时需要一定的资源。在计算机的内部,这两者体现为CPU运行时间和内存花销。
时间复杂度:
在明确时间复杂度的概念之前,我们必须明确一个规则。那就是复杂度存在的前提。我们假设计算机执行单一运算的时间相同,并不考虑硬件结构上的不同导致的运行差异。即我们认为,世界上所有类型的计算机都是标准计算机,其执行的单一运算(如加法、减法、乘法)均为标准运算,所花费的时间也是相同的。
所以,我们将时间复杂度定义为对某一标准输入数据执行某一算法后,所需要的时间长短。
可以被等价为,对某一标准数据输入执行某一算法后,所需要的步骤次数。
空间复杂度:
在计算机中,空间代表内存地址,此处的空间复杂度自然就是对某一标准数据执行某一算法后,所需要的内存空间,注意,这里的每次申请也被视为同样的空间复杂度,所以我们仍然可以近似的认为其可以替代为申请存储空间的次数。
所以,我们可以预先下一个结论,所有的算法优化,本质上都是节省计算步骤(无论是去掉冗余步骤还是将一个步骤处理的数据多次使用)
算法的好坏:
通过时间和空间复杂度,我们可以轻易的得出结论,那就是时间、空间复杂度越低,算法越好。
那又怎样标定每一种算法的好坏值呢?
我们引入
$$
最大时间复杂度:O(n)
$$
$$
最小(优)时间复杂度:\Omega (n)
$$
$$
平均时间复杂度:\theta (n)
$$
其中,我们在研究中使用最多的,是O(n);
在工程上,则会考虑平均时间复杂度。
为什么要学习算法:
既然标准库中已经提供了高效的数据处理支持,我们为什么还要学习算法呢?
当然是为了卷……
这里提出两个原因:
1.标准库无法覆盖到具体的业务场景。例如,我们需要对一颗庞大的多叉树进行局部数据修改,这个时候,我们处理的数据并不是标准数据,对于为了标准数据而书写的STL就不再高效。例如只要改动一个小节点,但是标准库就不得不去更新整个数据结构,更熟悉业务的我们自然不用这么干。
2.只有懂得实现原理,才能合理的使用工具。这里不再展开。
对数器的实现:
总所周知,算法的检验离不开数据,而随机数据发生器,就是在算法学习实践中检验的方法。它可以产生检验我们算法的原始数据。
当然,我们大可以在各种code平台上去检验代码,但是明白随机数据产生的原理,也是至关重要的。
总之,对数器的工作原理大概分为三步:
1.产生随机数据作为校验数据
2.使用绝对正确的方法作为校验方法
3.比较校验方法与被校验方法的输出是否一致
以下是随机数据发生的实现代码:
bool getRandomArrayOld(std::vector<int>& ioArray, int minValue, int maxValue,
int minLength, int maxLength)
{
bool res = false;
if (minValue> maxValue || minLength > maxLength || minLength <0 ||
(maxValue- minValue)>32757 ||(maxLength - minLength)>=32757)//不符合随机值发生要求
{
return res;
}
ioArray.clear();
srand(time(nullptr));//随机种子
int arraysize = ((rand() % (maxLength - minLength +1))+ minLength);
int arrayvalue;
while (arraysize> ioArray.size())
{
arrayvalue = ((rand() % (maxValue - minValue + 1)) + minValue);
ioArray.emplace_back(arrayvalue);
}
res = true;
return res;
}
bool getRandomArraySafe(std::vector<int>& ioArray, int minValue, int maxValue,
int minLength, int maxLength)
{
bool res = false;
if (minValue > maxValue || minLength > maxLength || minLength < 0)//不符合随机值发生要求
{
return res;
}
ioArray.clear();
std::random_device rd;//产生种子
std::mt19937 gen(rd());//梅森引擎
std::uniform_int_distribution<int> arraysizes(minLength, maxLength);
std::uniform_int_distribution<int> arrayvalues(minValue, maxValue);
int arraysize = arraysizes(gen);
int arrayvalue;
while (arraysize > ioArray.size())
{
arrayvalue = arrayvalues(gen);
ioArray.emplace_back(arrayvalue);
}
res = true;
return res;
}
其中,第二个随机数发生方法使用了C++11新特征,相比第一种方法具有随机数范围广、产生结果优质、数据不易破解的优势,建议在大数据量的情况下使用第二种方式。
C++11 新 random 库提供了三个随机数引擎 [linear_congruential_engine] (线性同余引擎),[mersenne_twister_engine] (梅森旋转引擎) 和 [subtract_with_carry_engine] (带进位减)。
匹配两个数组是否相等的代码实例如下:
template<typename T>
inline bool IsSame(std::vector<T>& ioArray1, std::vector<T>& ioArray2)
{
bool res = true;
if (ioArray1.size() != ioArray2.size()) return false;
for (size_t i = 0; i < ioArray1.size(); i++)
{
if (ioArray1[i] != ioArray2[i])
{
res = false;
break;
}
}
return res;
}
稍事休息,下一节,我们将从排序算法开始,正式开始介绍算法内容。
下一节导航:基础排序算法归纳1
Q.E.D.