曲线数学表达
前言
资料来源于网络,如有侵权请告知删除
图片资源挂载于github,若无法加载图片请检查网络
如有错误,清留言斧正
贝塞尔曲线
在讲述贝塞尔曲线的发展与表达之前,我们先回顾一下直线的表示方式。
回到小学数学,假设我们有两个点,他们相连即可构成一条直线。
用式子表达为:
$$
{\rm}(t) = t + (1 - t)
$$
仔细观察此时的t,我们已经完成了在计算机图形学中一个非常重要的表达方式:插值(lerp)
当然,我们提出这个概念肯定不是为了画一条直线……
我们可以画很多条直线,比如这两条:
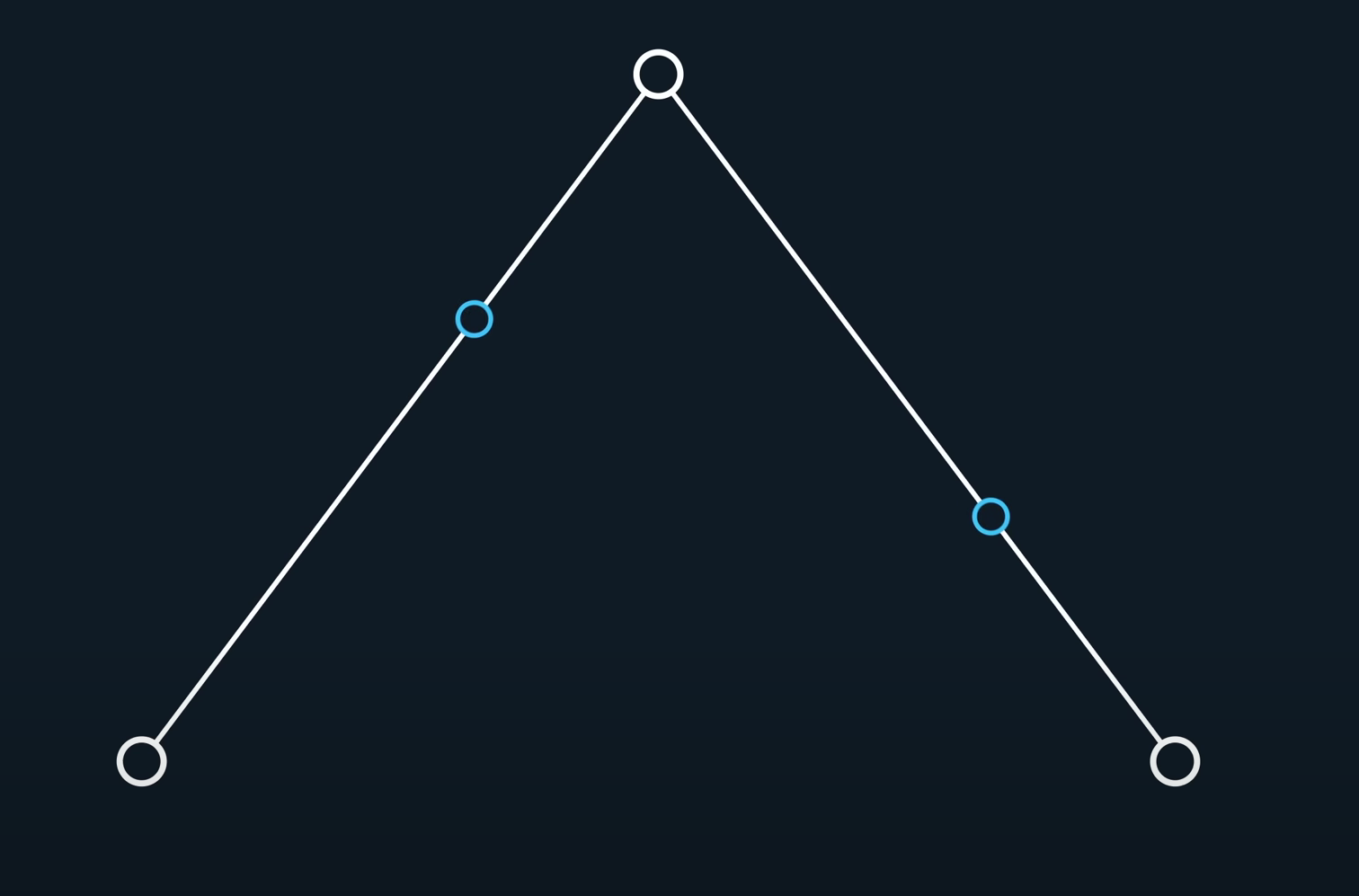 然后,我们可以连接这两个点,在使用一次lerp,此时,随着t的变化,这个点在二维平面中也随之变化
然后,我们可以连接这两个点,在使用一次lerp,此时,随着t的变化,这个点在二维平面中也随之变化
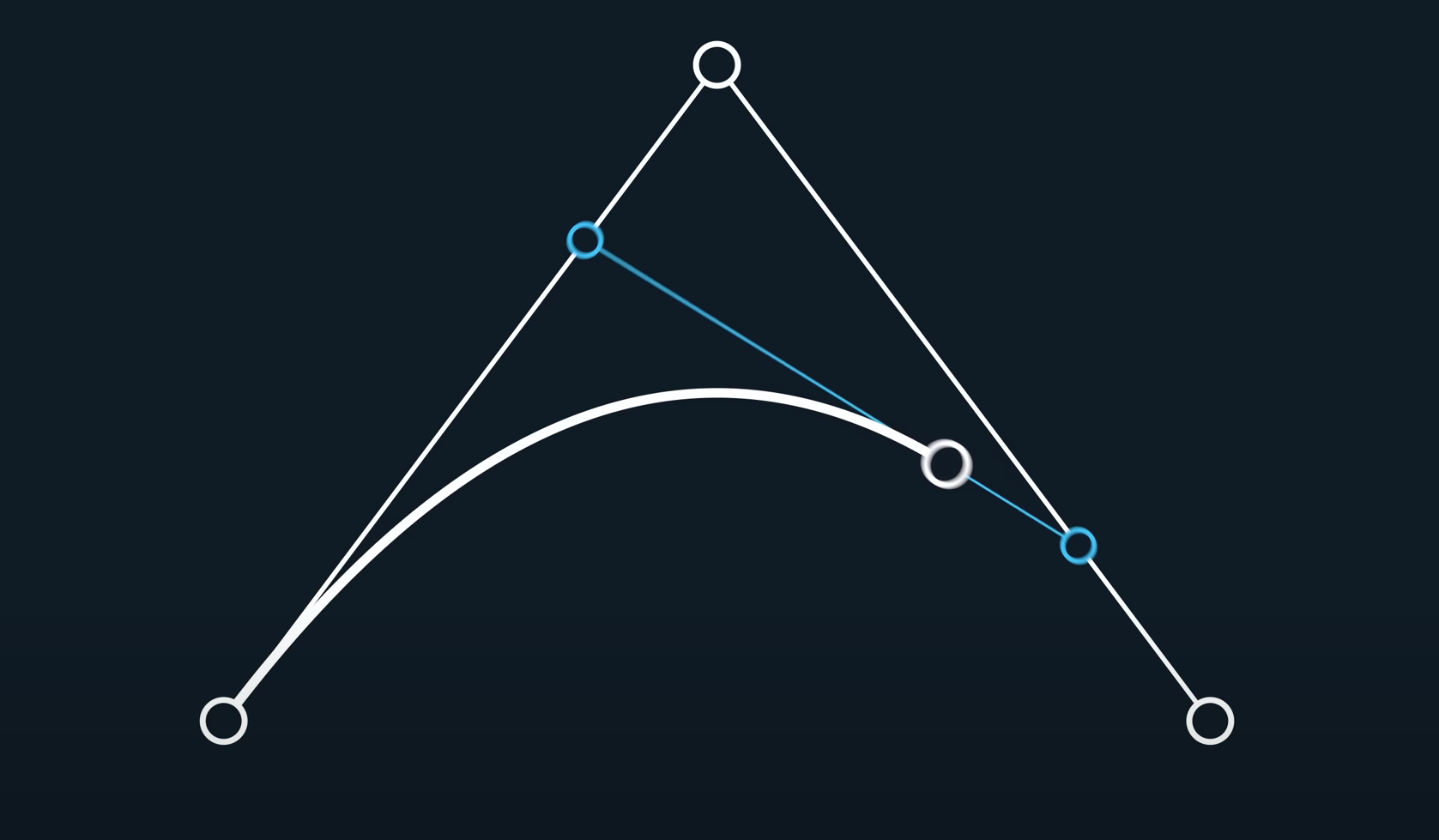
于是,我们画出来了一条曲线,这个,就是经典的贝塞尔曲线。好了,讲完了(不是……)
接下来,才是我们正式开启曲线表达方式的旅程。
几种解释方式
曲线的表达是公式,而公式可以被写成许多种方式,下面我们介绍常见的表达方式:
lerp+递归
按照之前我们提到的绘制曲线的方式,从两点构成直线,到三个点画出曲线,我们可以加入更多的点,绘制出来的曲线也如出一辙:
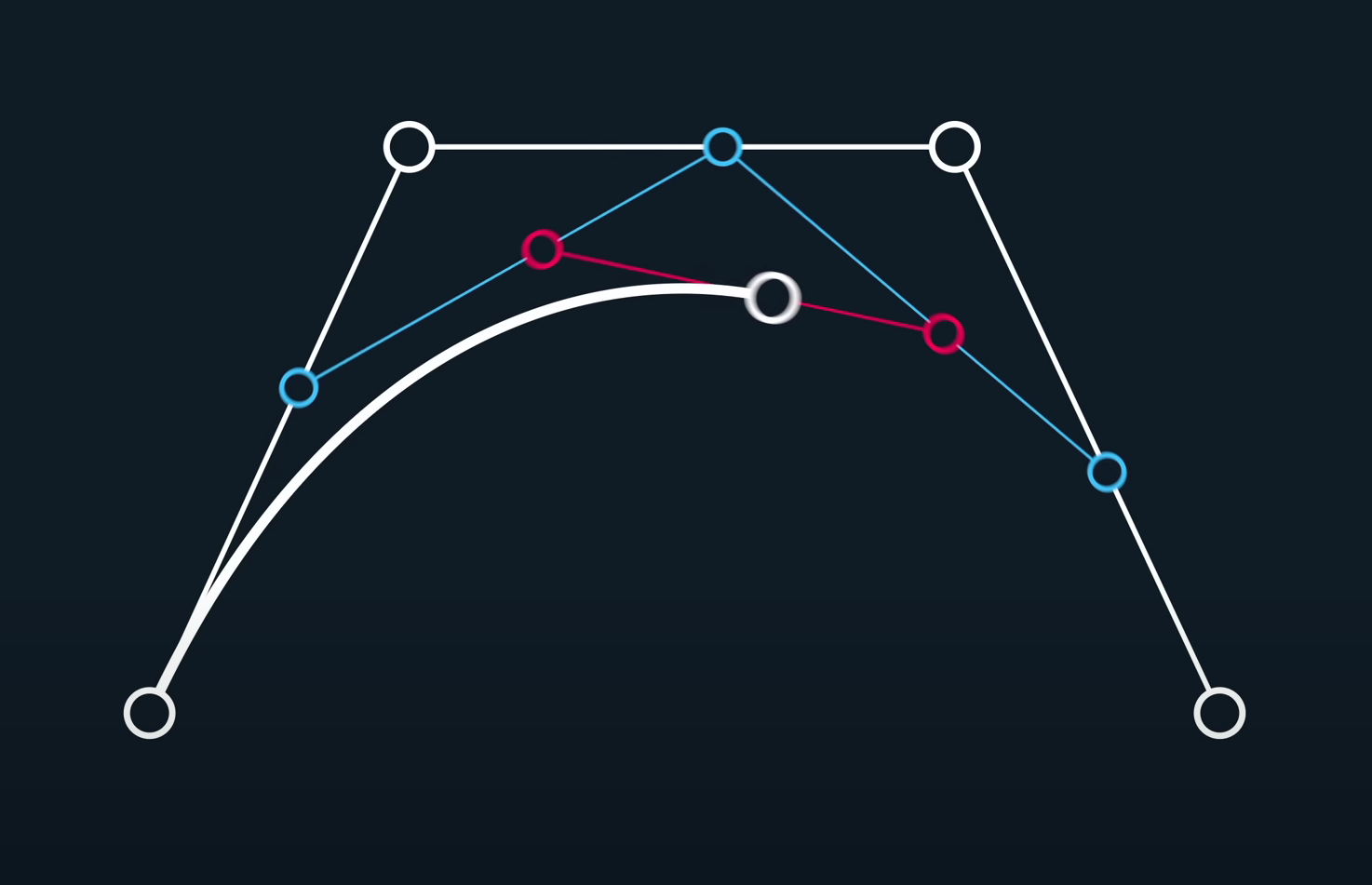
这样的方式,我们称之为插值递归法。数学表达如下:
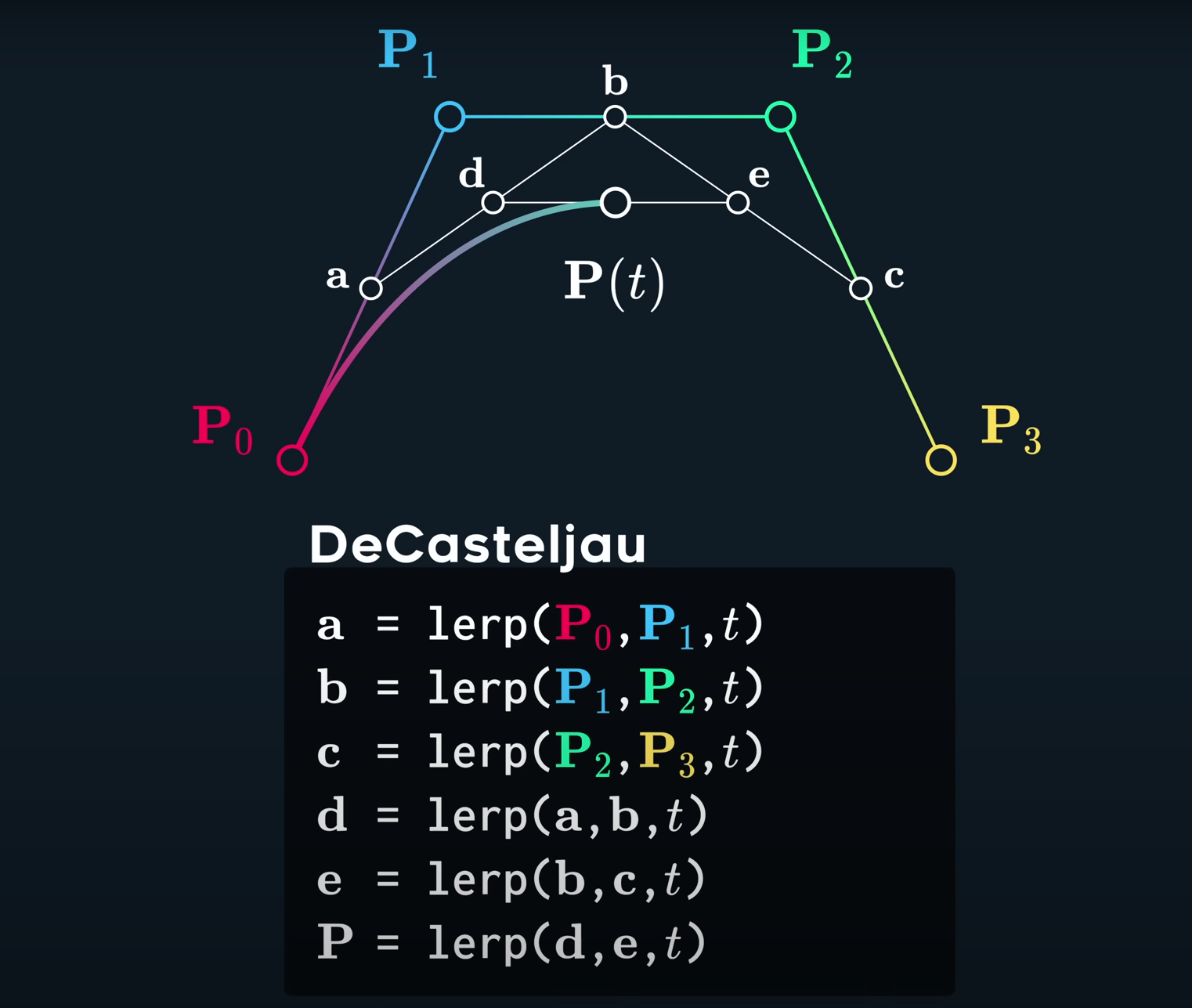
非常符合计算机直觉,但是,递归终归是一种昂贵的行为。所以我们也提供其他的表示方式。
Bernstein(基函数表示)
我们先放一张图:
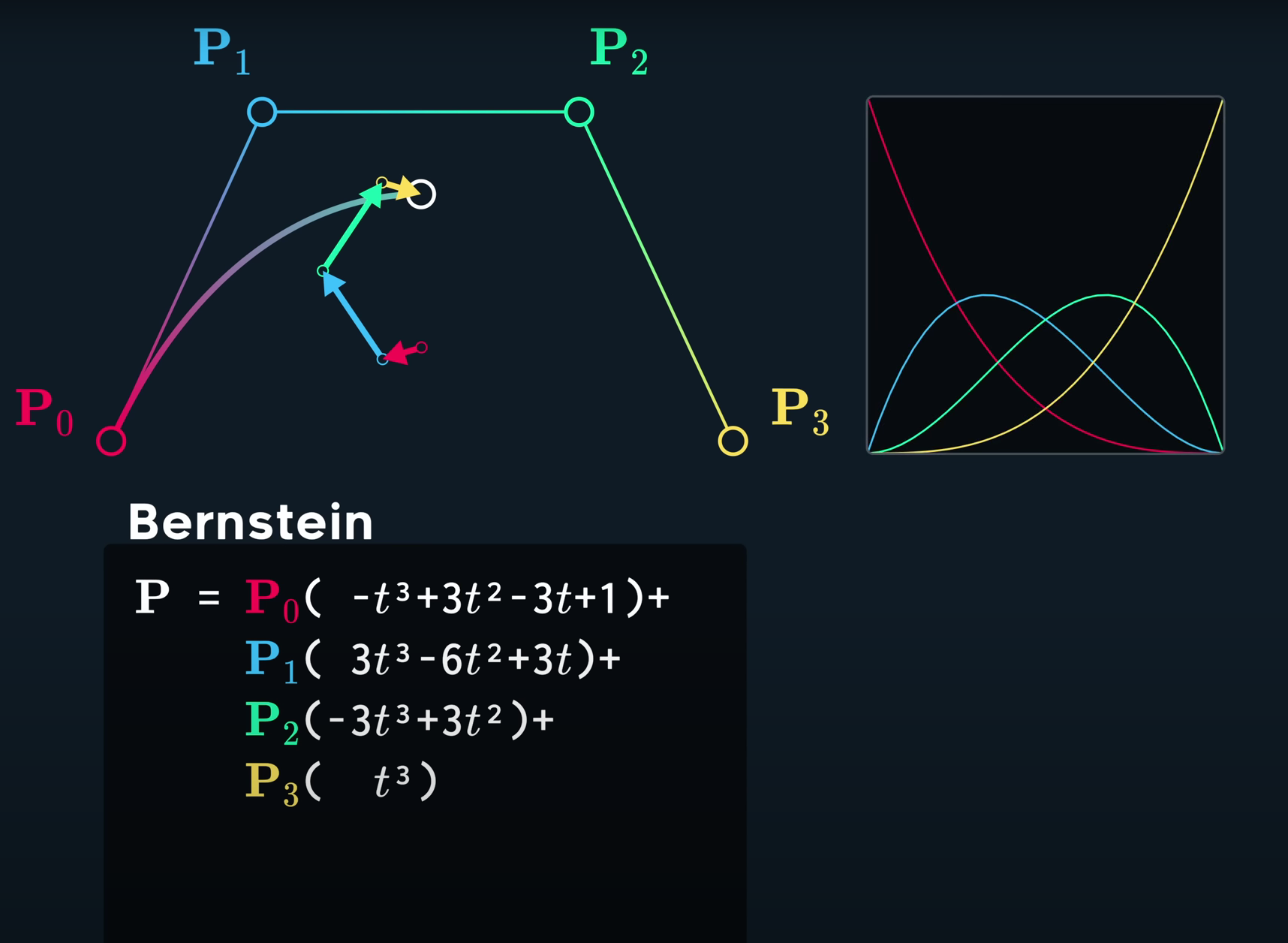
这个就是国内大多数的教材在描述贝塞尔曲线时给出的解,可以看到,我们将每一个控制点单独列出来,并且每一个控制点所带的参数都是一个t为变量的方程。这样的方程组称为Bernstein基函数。
它们各自表示什么意思呢?
我们看向旁边的基函数曲线部分,我们可以将它理解为一种权重,或者“影响力”。
当t的参数函数值很大的时候,它乘以一个点,所得到的结果会靠近这个点,或者说(拉取)这个结果点【前提是所有的参数方程加起来的结果为1】
也就是说,在这个式子里面,我们有三个方向的力作用到结果点上面,这可以理解为Bernstein基函数的通俗解释方式。
polynomical coefficients(多项式系数)
既然我们可以用它组成以控制点为核心的基函数,那我们当然也可以将T提取出来,组成新的多项式
当然,还是先上图
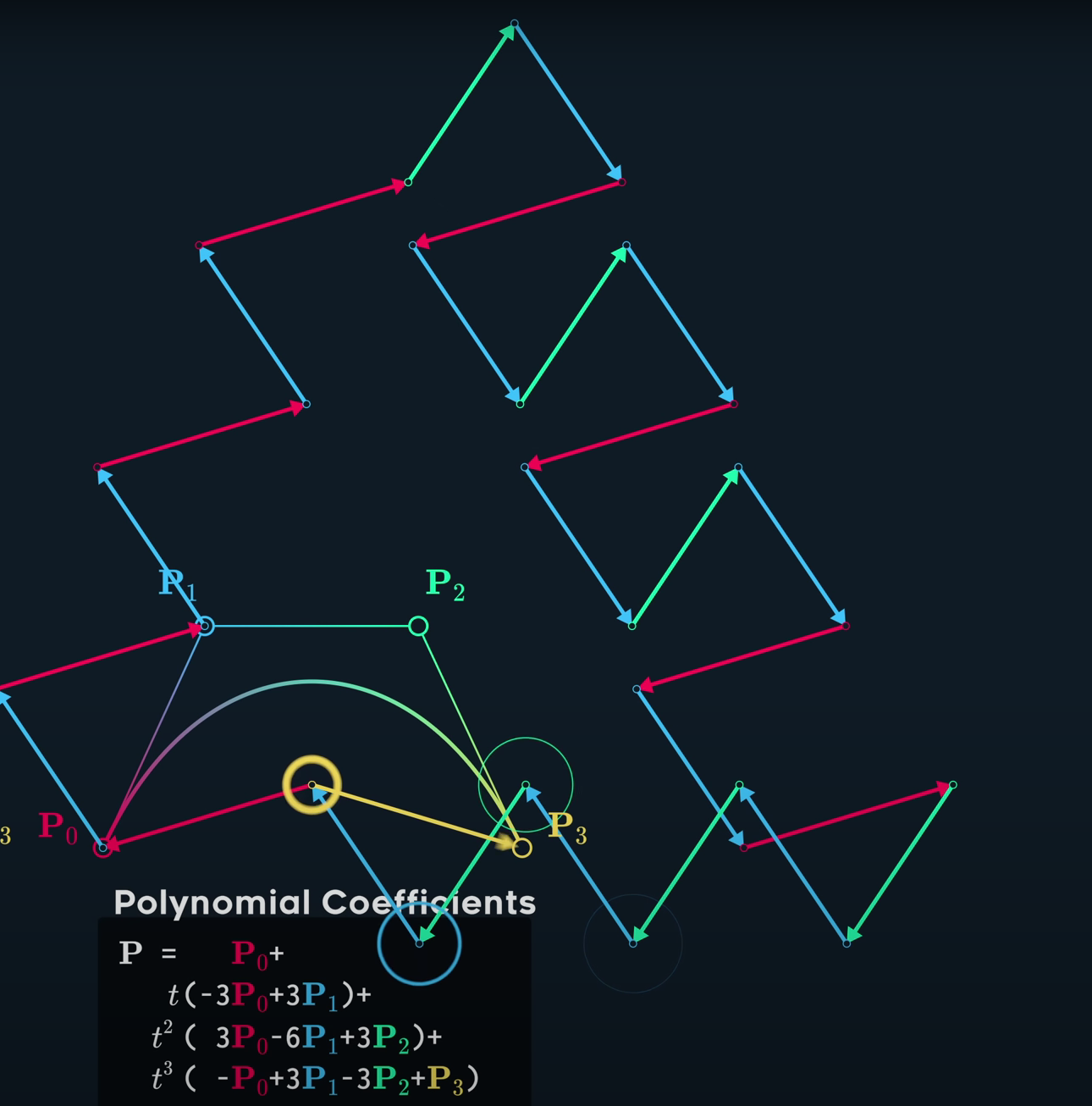
由于系数变成了控制点,所以我们可以看到随着自变量t的变化,控制点所表示的系数却没有变化,
但是它仍然以类似(拉扯)的方式影响结果点,每一个系数的拉扯都是以控制点为最小单位的向量。
martix线性代数表示
挡然,你肯定已经发现了,使用一个简单的矩阵就可以完美的描述这个问题。线性代数的表达往往完备且优雅:
如图:
但这并不意味着其他方式不重要,相对于单纯的数学表达,带有显著物理特征的表达方式会有别样的美感。
我们这里放一张全家福吧:

主要应用场景
PS\设计软件等
贝塞尔曲线的优缺点
优点
光滑、连续、优雅……很适合一锤子买卖
缺点
1.lack local contorl
很显然,我们使用多项式系数表达贝塞尔曲线的时候,可以发现,每一个结果点都会收到每一个控制点的影响,这几乎是无法忽视的问题
假如我们每增加或者移动一个控制点,整条曲线就一起摇摆,那这曲线也太过于自由了。完全融入不了严肃的工作场景
2.没有精确地路径点
这一点来源于其计算性质,由于它受到了过多的“拉扯”,所以我们并不能让它通过某一点,出非精确计算达成某种巧合,
但是这个功能无论是在工业软件还是在游戏中都是十分重要的。
3.不稳定(指修改控制点时)
这一点和第一点可以算是师出同门了。我们急需一种方式约束他
4.计算困难
贝塞尔曲线的计算难度将随着阶数上升而显著提升
B样条
相信我们谈论了这么久的贝塞尔,你们一定猜到它不是重点
当然,由于贝塞尔曲线过于固执和不可控,它很难用于工业设计或者游戏设计领域,只能辅助人们做做PPT之类的活儿。
但是样条,他不一样。
样条的定义
样条,是早期人们在设计过程中为了得到自己想要的设计效果,利用细线、软管和一些固定方式扭曲得到的细长条。
我们现在借用这个词来描述曲线。
U的含义
正如大家想象的那样,样条线是使用类似压铁之类的外部工具进行曲线造型。
每次用一个压铁固定一段样条时,我们就会认为的将一条曲线分为两个部分,或者反过来说,把两条曲线拼接到一起。
诶……是不是想到了什么。如果说贝塞尔曲线被抛弃的原因是它不受控制,如果它足够短,那不受控就不受控吧,我们把这些
“元素”连接在一起,不一样可以拼接出曲线吗。可以说,这个想法也相当的计算机。
于是,每一段的曲线我们把它成为u,一条曲线将以u1,u2,u3等联系在一起。
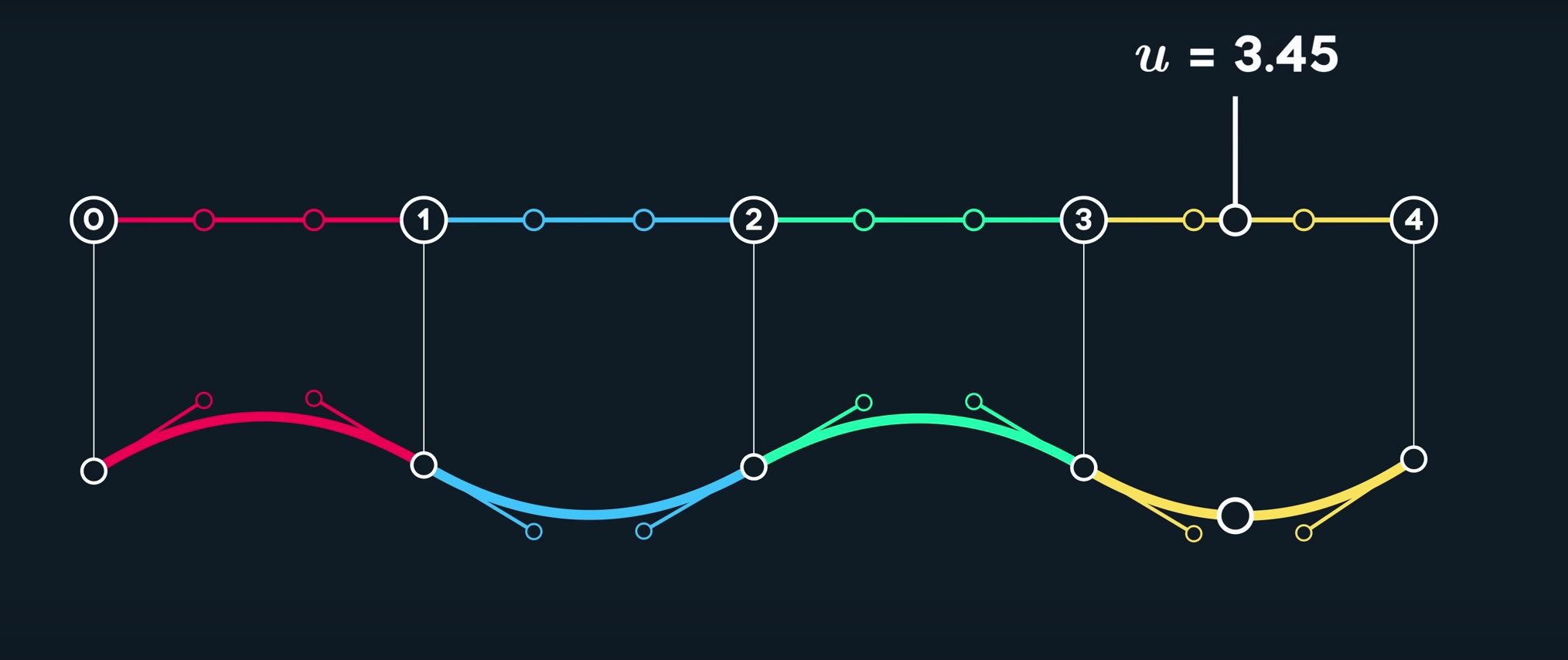
contorl point & knots
我们将简单的三阶贝塞尔曲线相连,获得以下示意图:
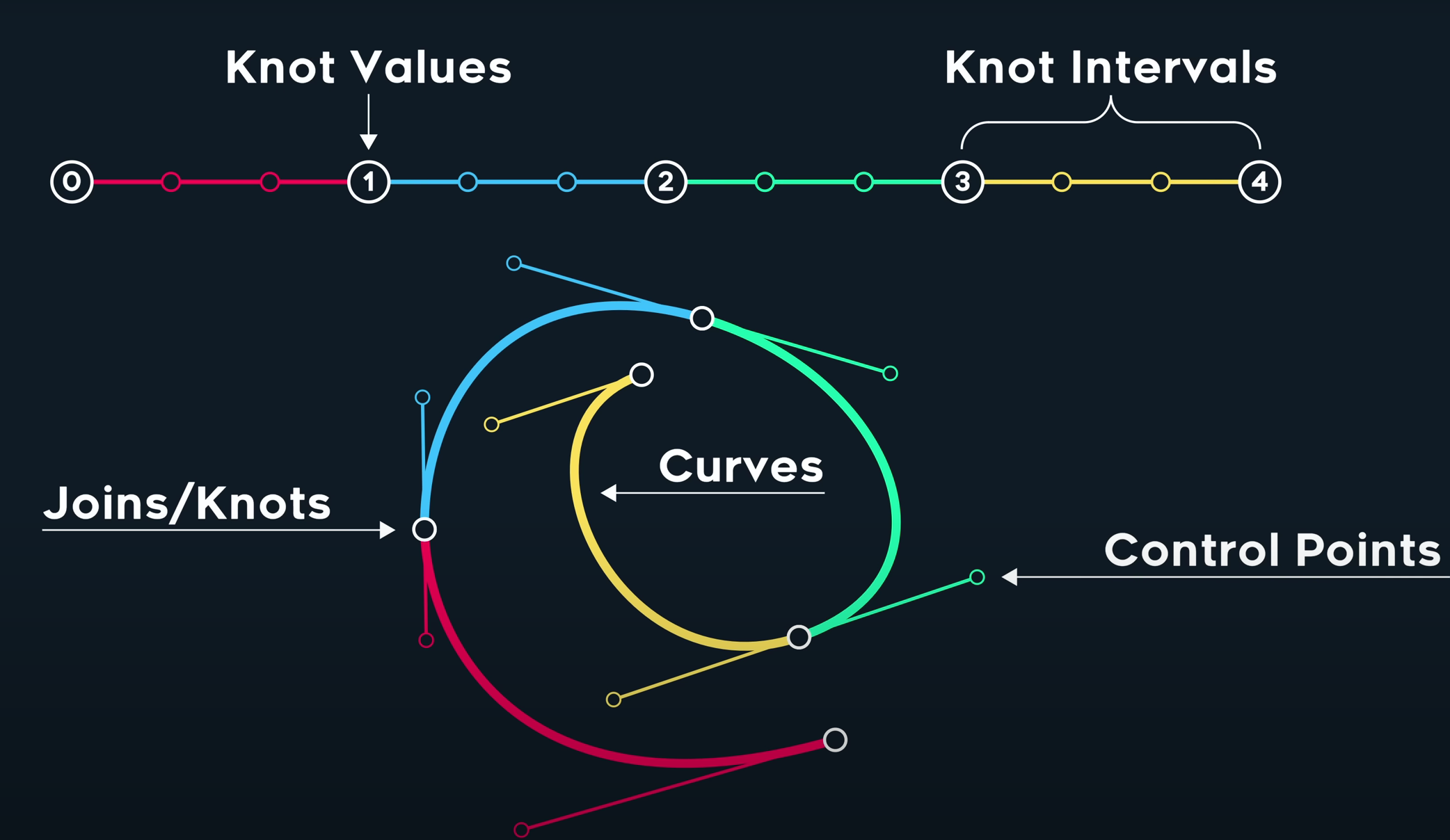
相比之前的原始曲线,我们看看新的曲线有没有解决上面的四个问题?
1.它使得我们能够在节点(连接处)对曲线进行调整,同样的,也可以在控制点处进行调整,无疑解决了缺少控制点的情况。
2.精确路径点的问题,可以使用节点来解决。我们可以调整节点的位置,来使得曲线通过我们希望的方位。
3.不稳定的问题,是由不同曲线相连的方式解决的。由于分段曲线之间相互独立,所以不存在改变一个点,全局跟着动的情况
4.计算代价的问题,由于整条曲线由很多条三阶贝塞尔曲线相连而成,三阶贝塞尔曲线本身的计算开销低,连在一起也不会指数级上升。
由此来看,将3阶贝塞尔曲线相连仿佛是神之一笔,但是,这样就解决所有问题了吗?
虽然我们使用连接低阶贝塞尔曲线的方式规避了之前提出的问题,但是一条曲线终究是要落到实际的应用中。
我们接下来要讨论的就是关于曲线在应用中最重要的性质:连续性
样条线连续性分析
如果说样条线是由多条贝塞尔曲线相连形成,那么连接点必然是需要重点讨论的。
简单的连段相连,我们可以分为断开(broken)、接触(touch)、相接且切线同向(aligned)、相接且切线矢量相等(mirrored)。
连续性分析的物理意义
在游戏中,我们规划出一条曲线,可能是汽车的运动轨迹或者人物的行走轨迹,那么人物会以什么样的方式运动就是重点了。
我们在初中物理中学过,以时间t为自变量,路程l为因变量的一阶方程,其中,一阶导数为速度、二阶导数为加速度。
现在,我们把曲线看做一段距离,什么样的连接方式可以保证匀速、什么样的方式可以保证速度变化合理就是我们需要讨论的话题了。
连续的重要性
knots & alinged &mirror
连续性分析的应用场景
C连续与G连续
为什么我们要强调一条曲线的连续性?因为曲线的连续性在很大程度上决定了这条曲线的可用性。无论是工业设计、游戏开发、美术创作,我们都需要考虑在实际场景中赋予曲线特征的含义、比如形体、颜色、路径……
因此,能否让曲线符合我们所需的物理场景就是我们需要关心的内容了。
C0
倘若线段之间完全不相连,则不具备连续性。如下图的线段:
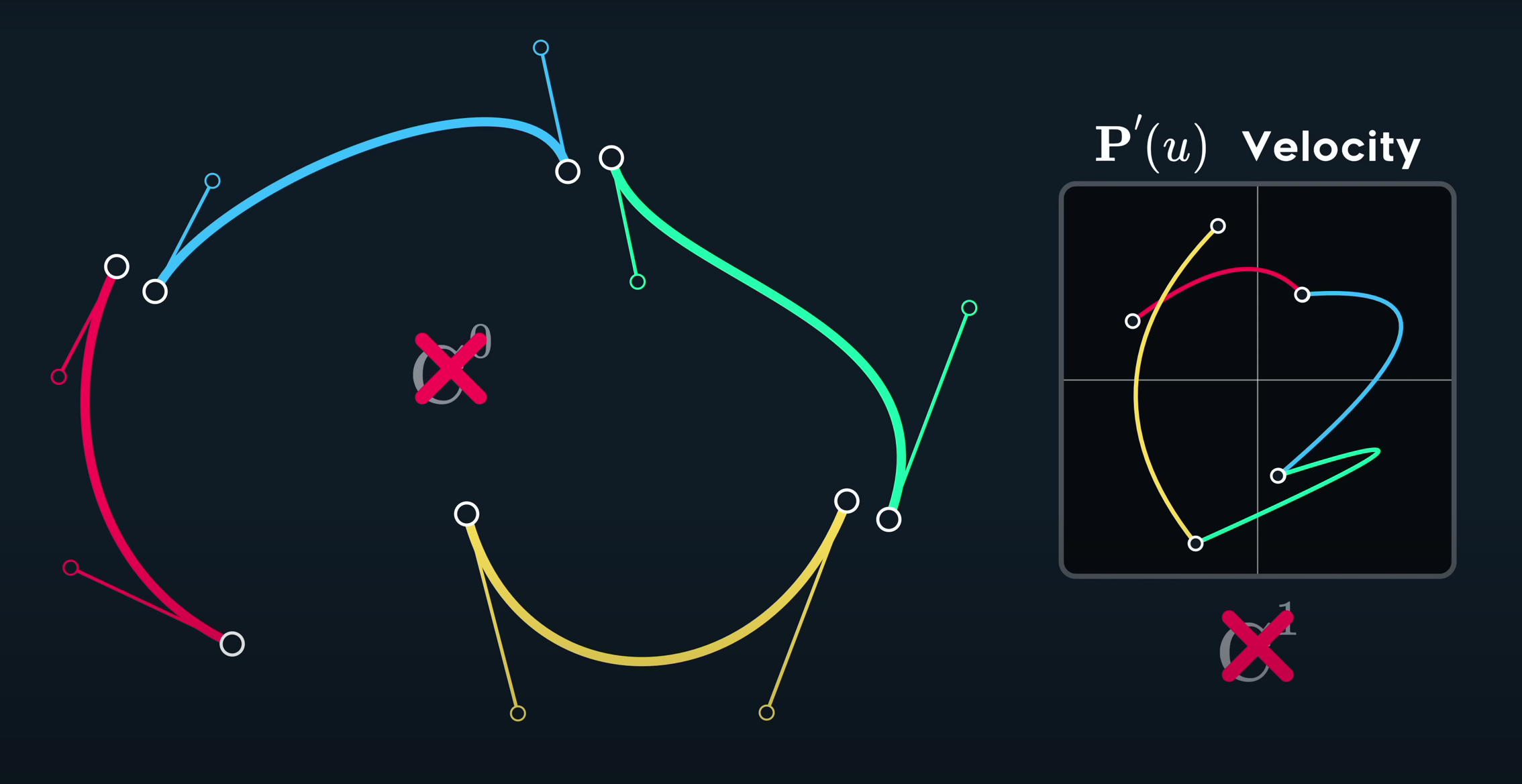
C1
c1的含义是曲线的一阶导数、或者是速度是连续的,注意,这里并不会同时要求C0连续,因为路径断开一样可以满足速度连续的要求
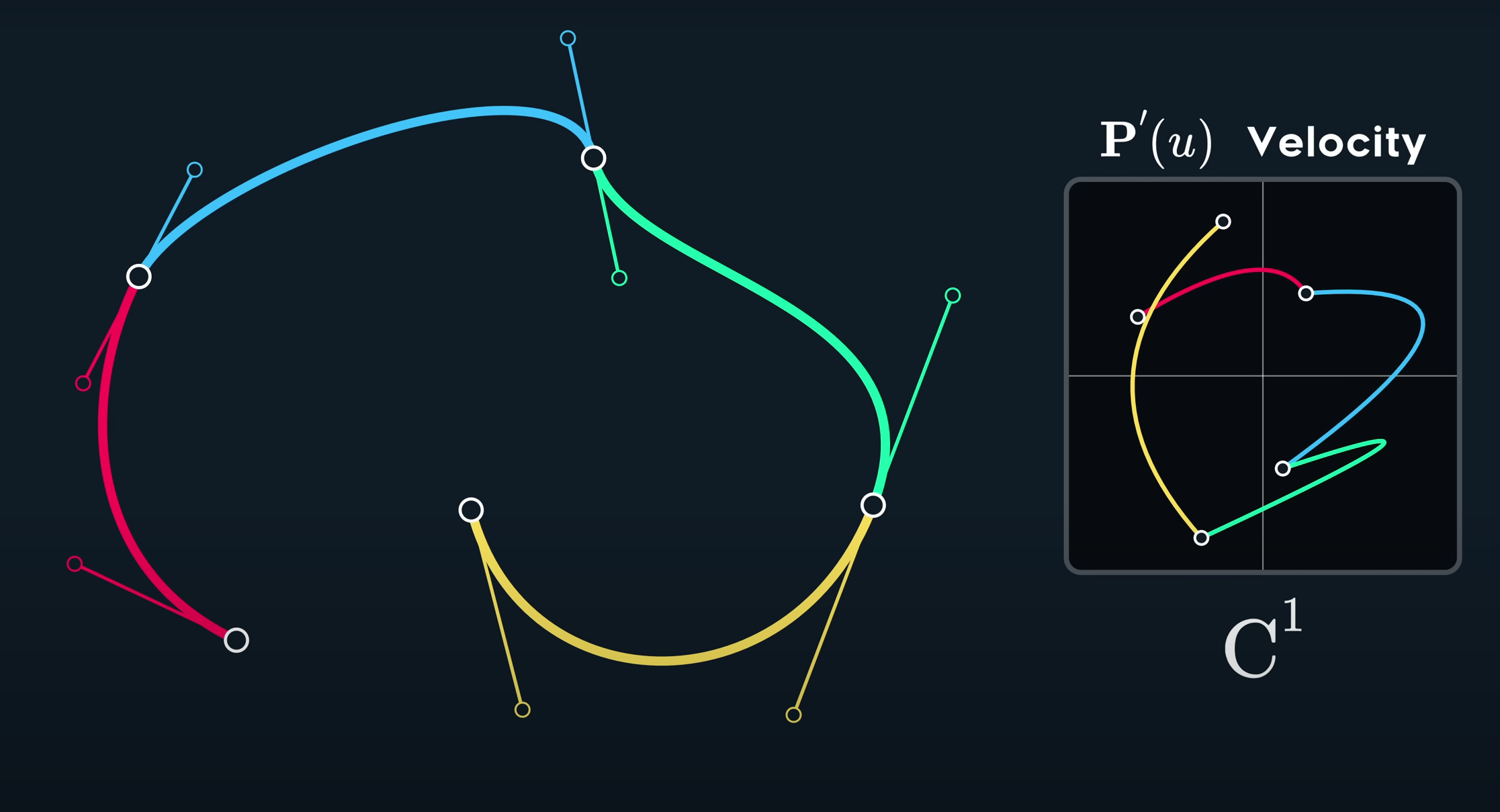
C2
如果说C1连续关心的速度是一阶导数,那么C2连续所关心的就是二阶导数,一阶导数我们可以用两个点连线计算出,而二阶导数就需要至少三个点了
所以我们需要当前点以及前面两个点加在一起才能完成二阶导数、也就是加速度的约束。
也就是说,我们需要牺牲一些控制自由度来完成这件事情,如下图:
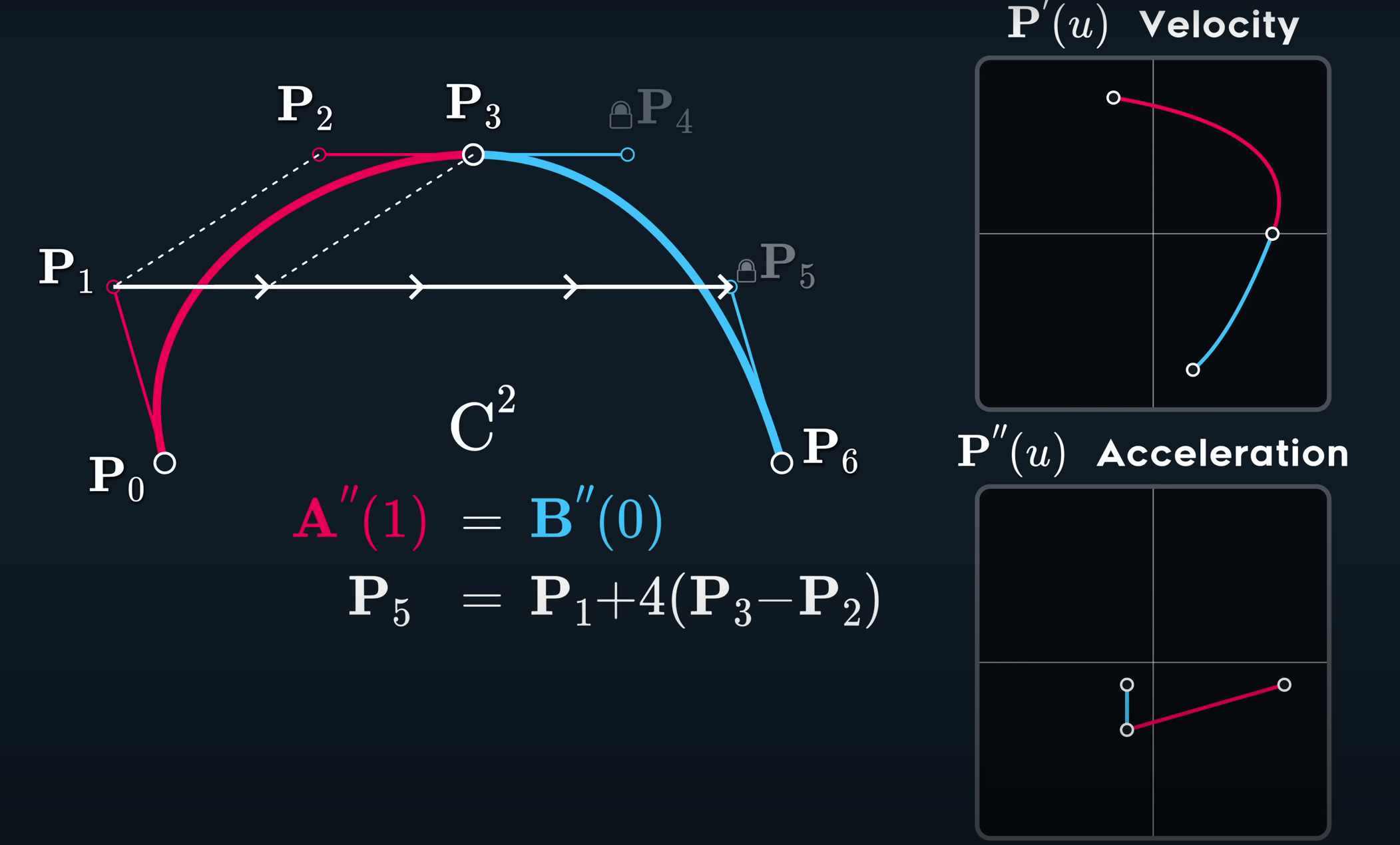
C3
C3连续关心的是一种变化率的连续,英文里是jolt,这要求我们用当前点以及至少三个前置点去构建约束。
而巧合的是,我们使用的连接单位曲线时三阶的贝塞尔,也就是说,如果我们想要在当前的条件下实现C3连续的话,我们将锁死所有的可控点,如图:
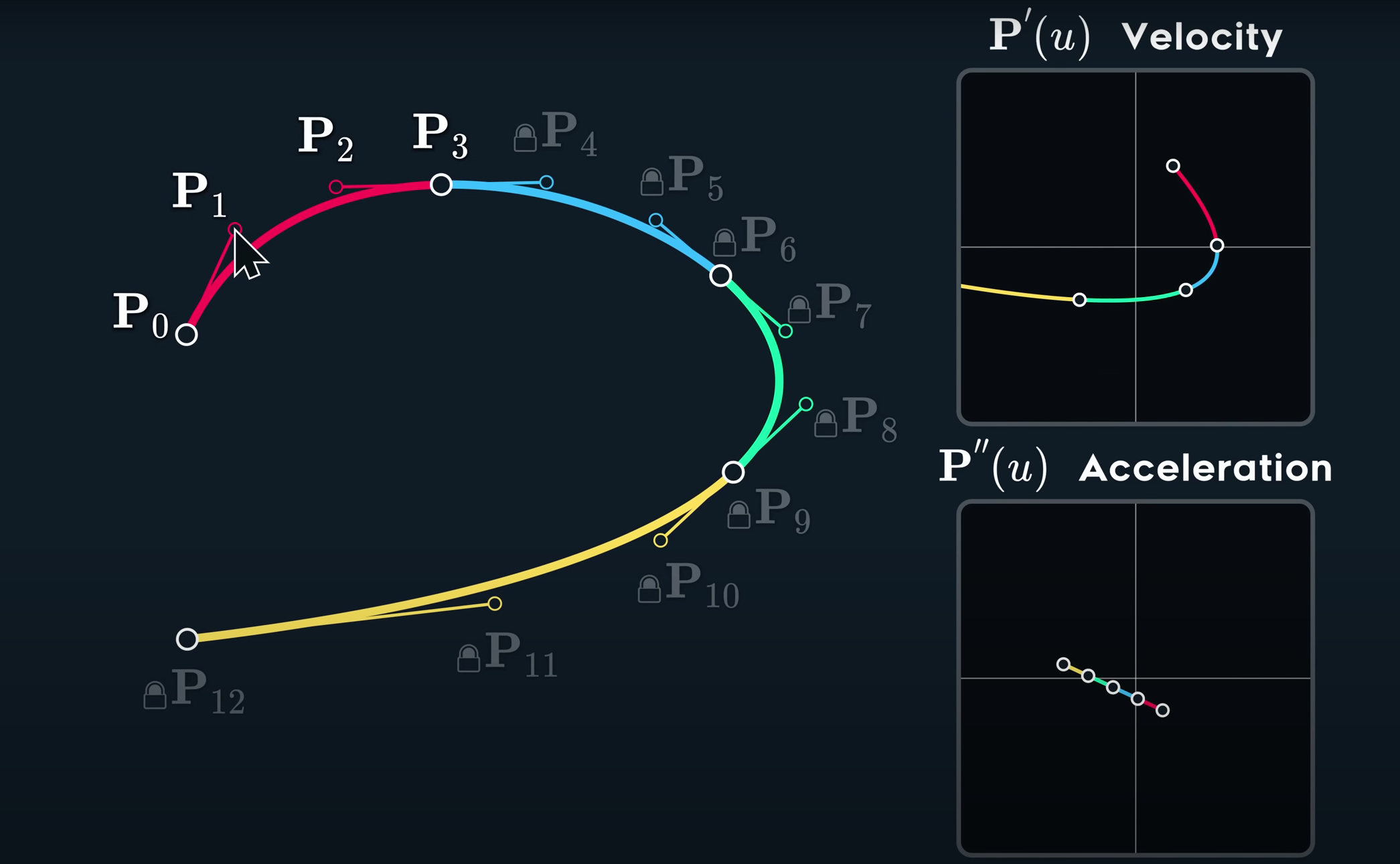
也就是说,在不进行其他改变的情况下,曲线已经变成了一条贝塞尔曲线。换言之,他也是C无穷连续的曲线。
如果我们需要C3连续,就不得不升阶最小单位曲线。幸运的是,我们一般不会使用这么高连续性的曲线。
C与G
如果说,速度和加速度是物理运动的维度考量曲线,那么从设计角度来看,我们刚刚讨论的东西毫无用处
在设计中,我们往往只关心它长什么样子,也就是形体怎么样。
此时,我们就要引入一个工业设计中常用的概念,叫“光顺”,什么叫光顺,我们开灯看一下;
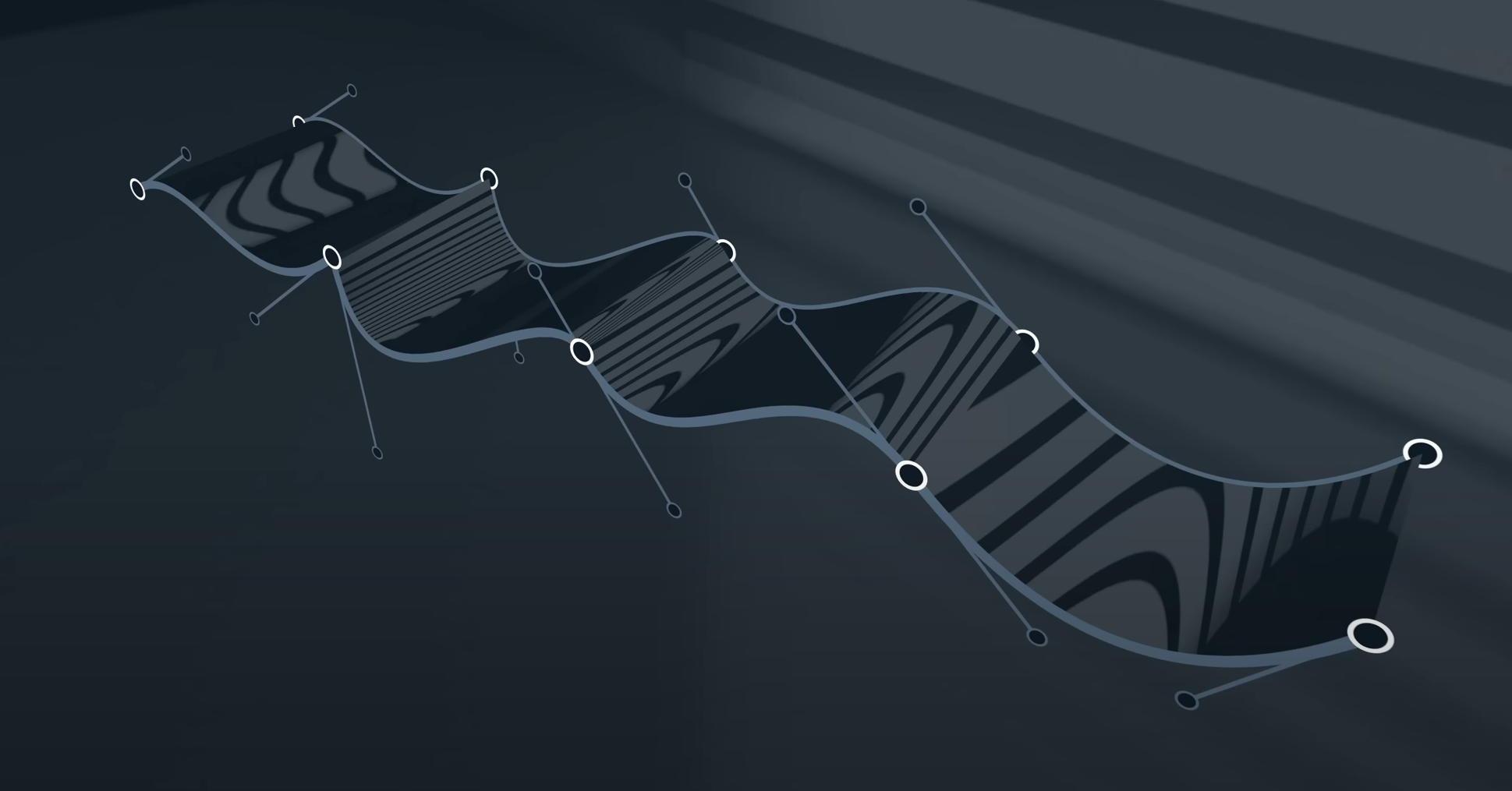
在这张图片中,我们使用了C0连续的曲线进行拉伸,并且加上了光源,此时,我们可以看到,在光的照射下,整个形体并不是很“丝滑”
这就是我们追求光顺的主观原因。
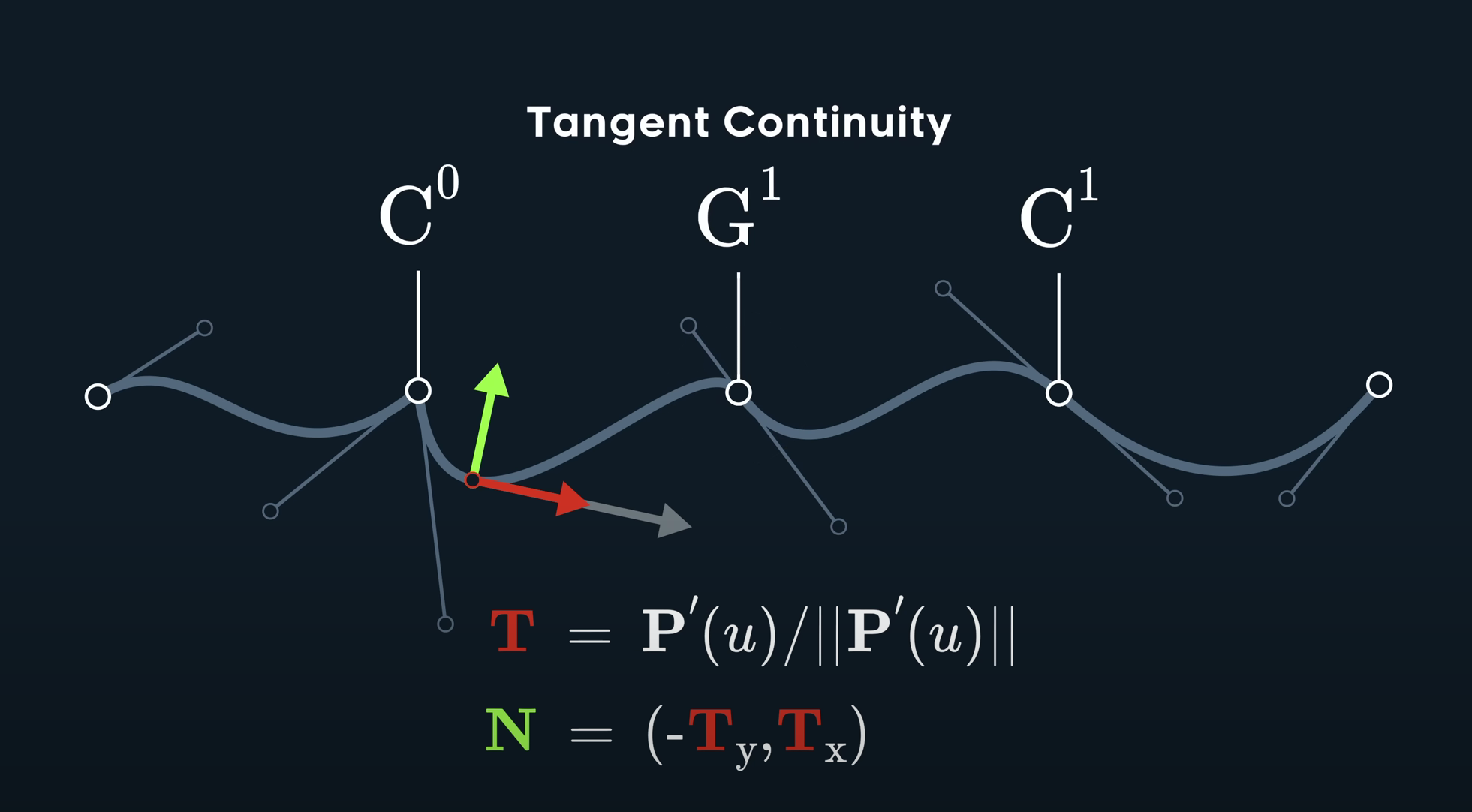
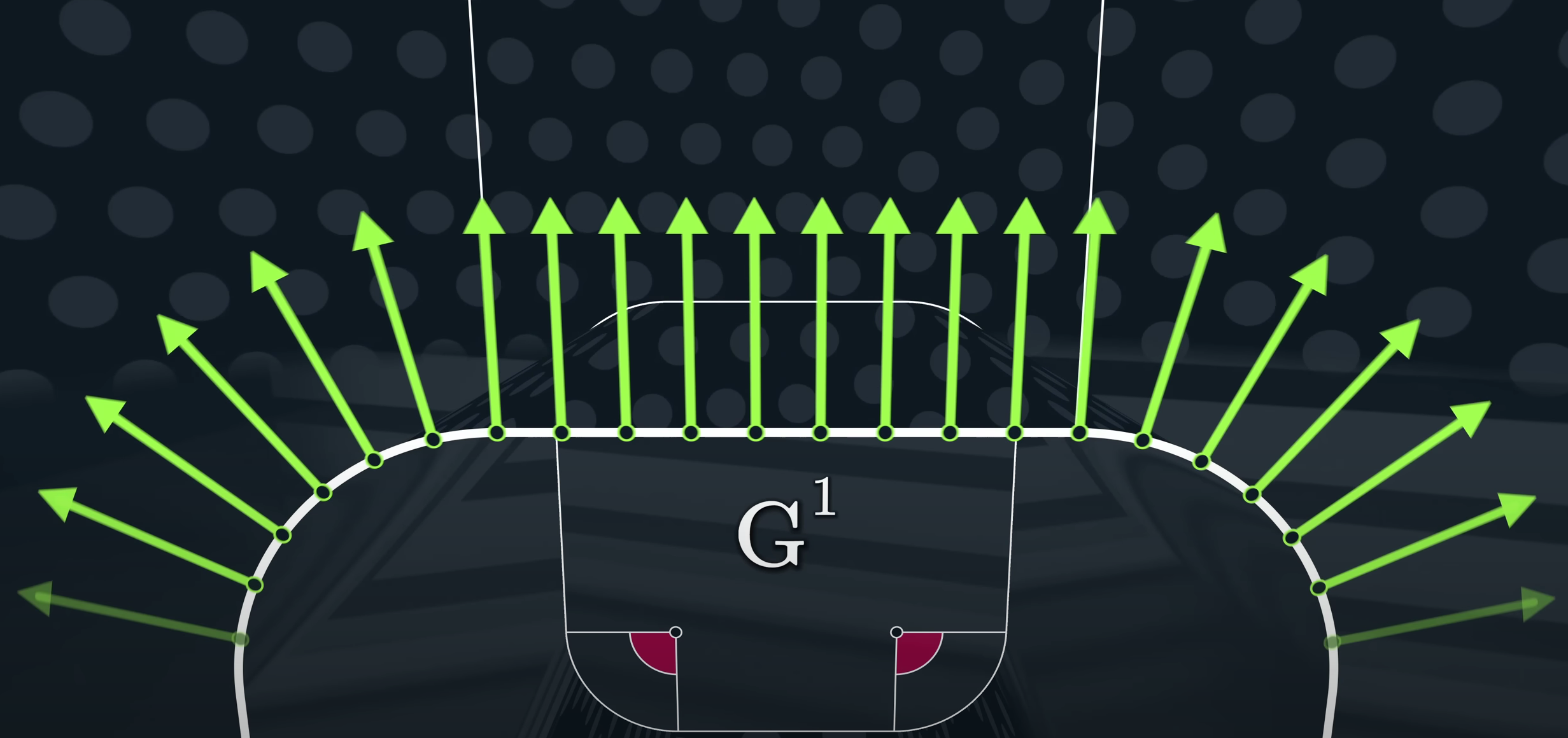
G1
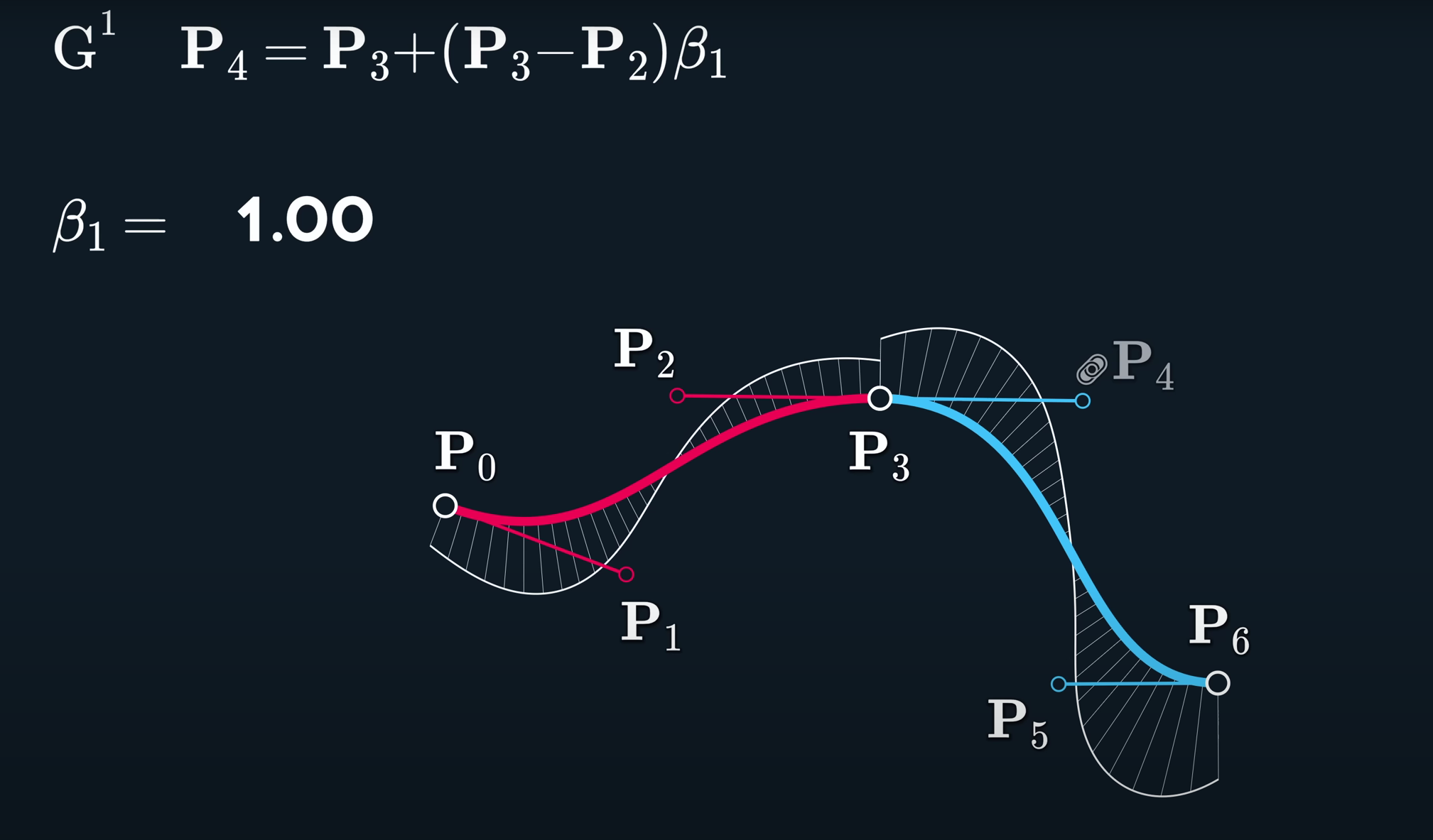
G2

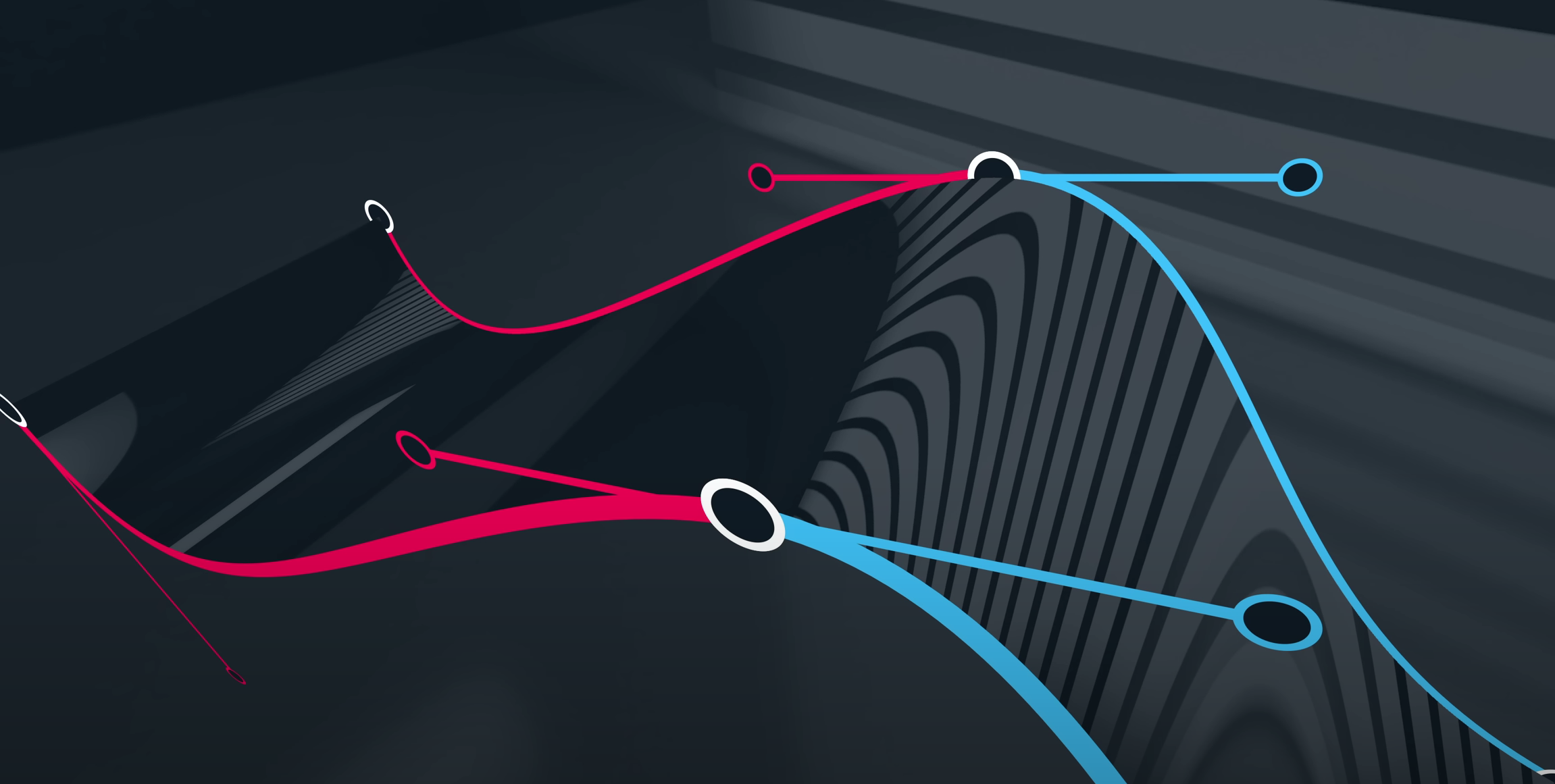
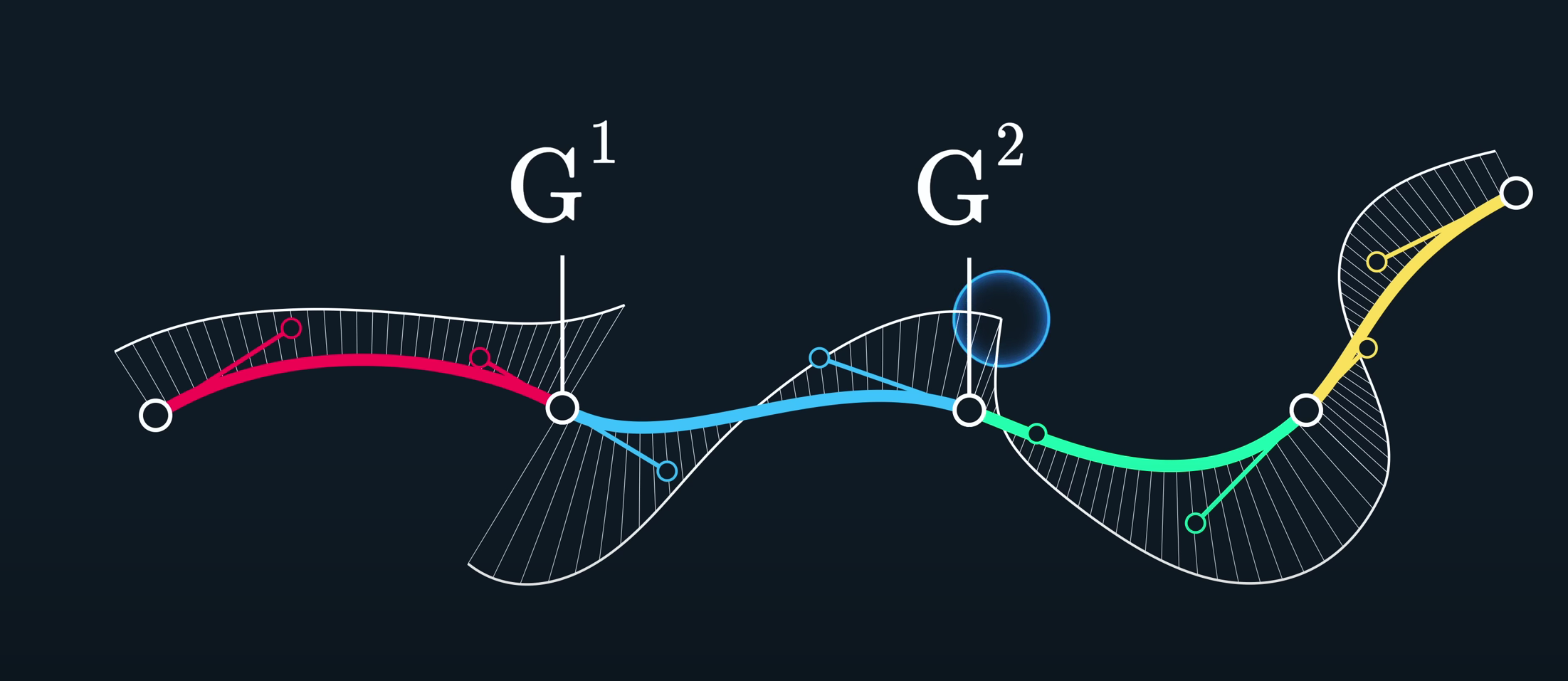
G3
B样条的数学表达
linear

Hermite
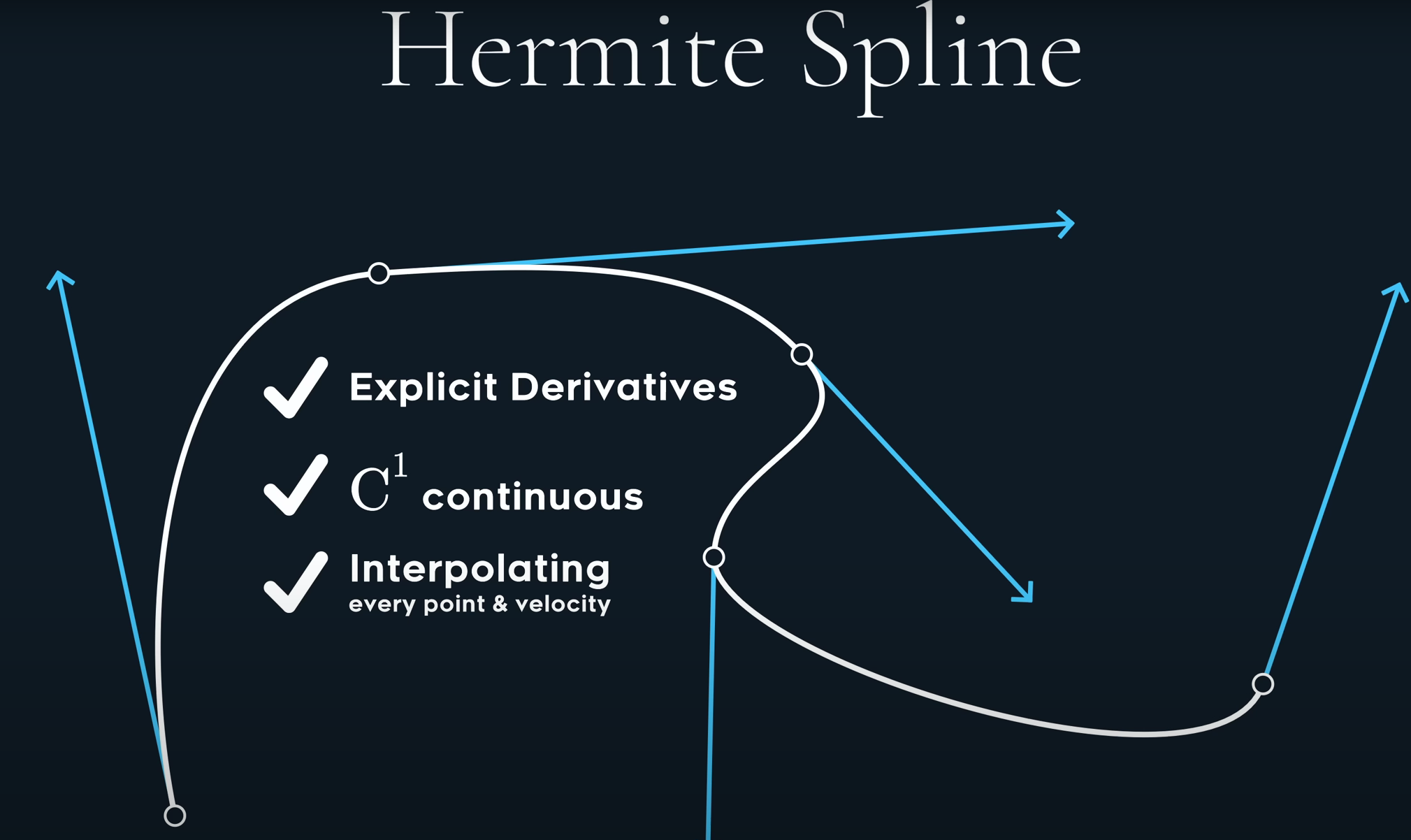
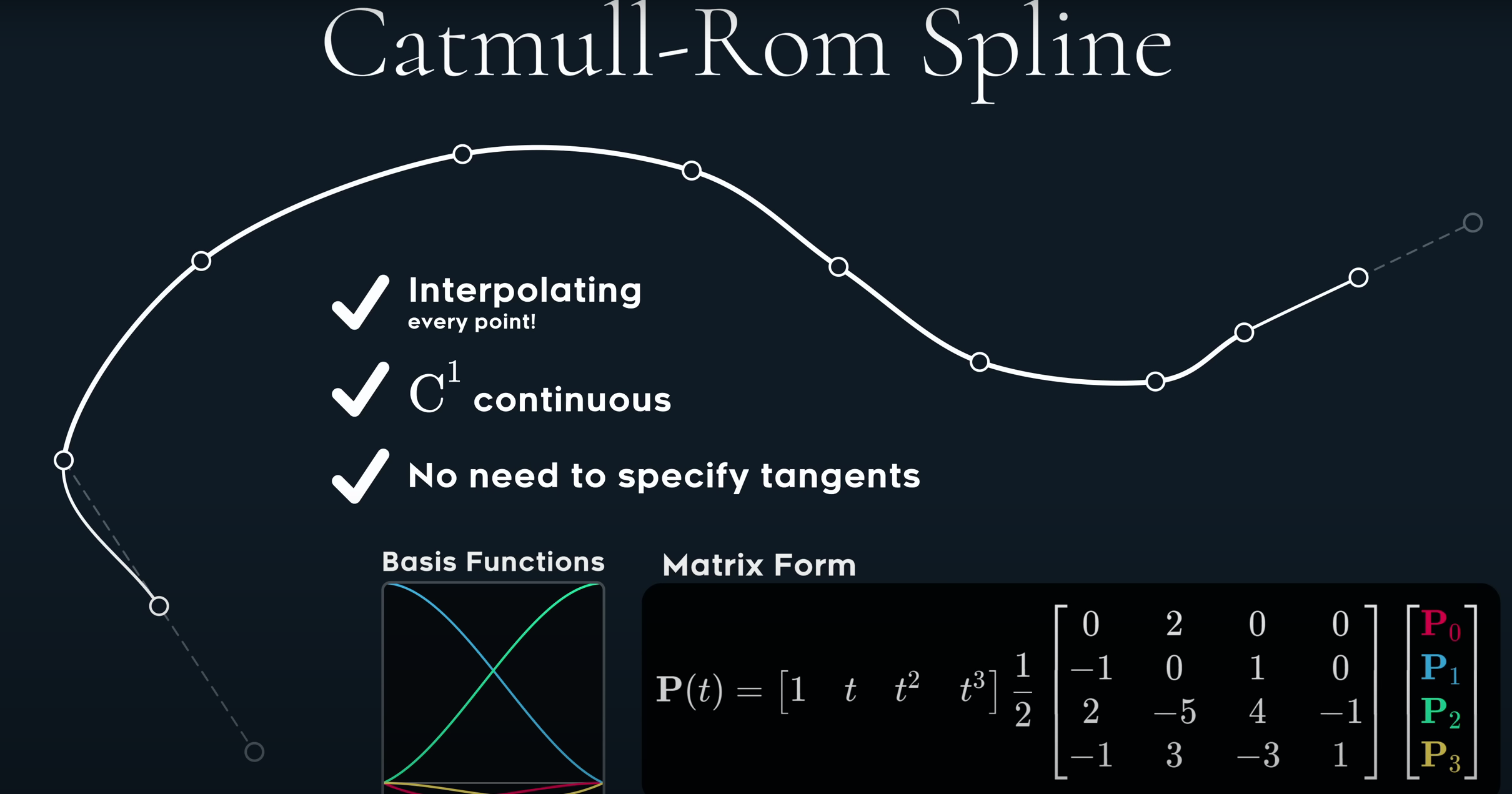
Catmull-Rom
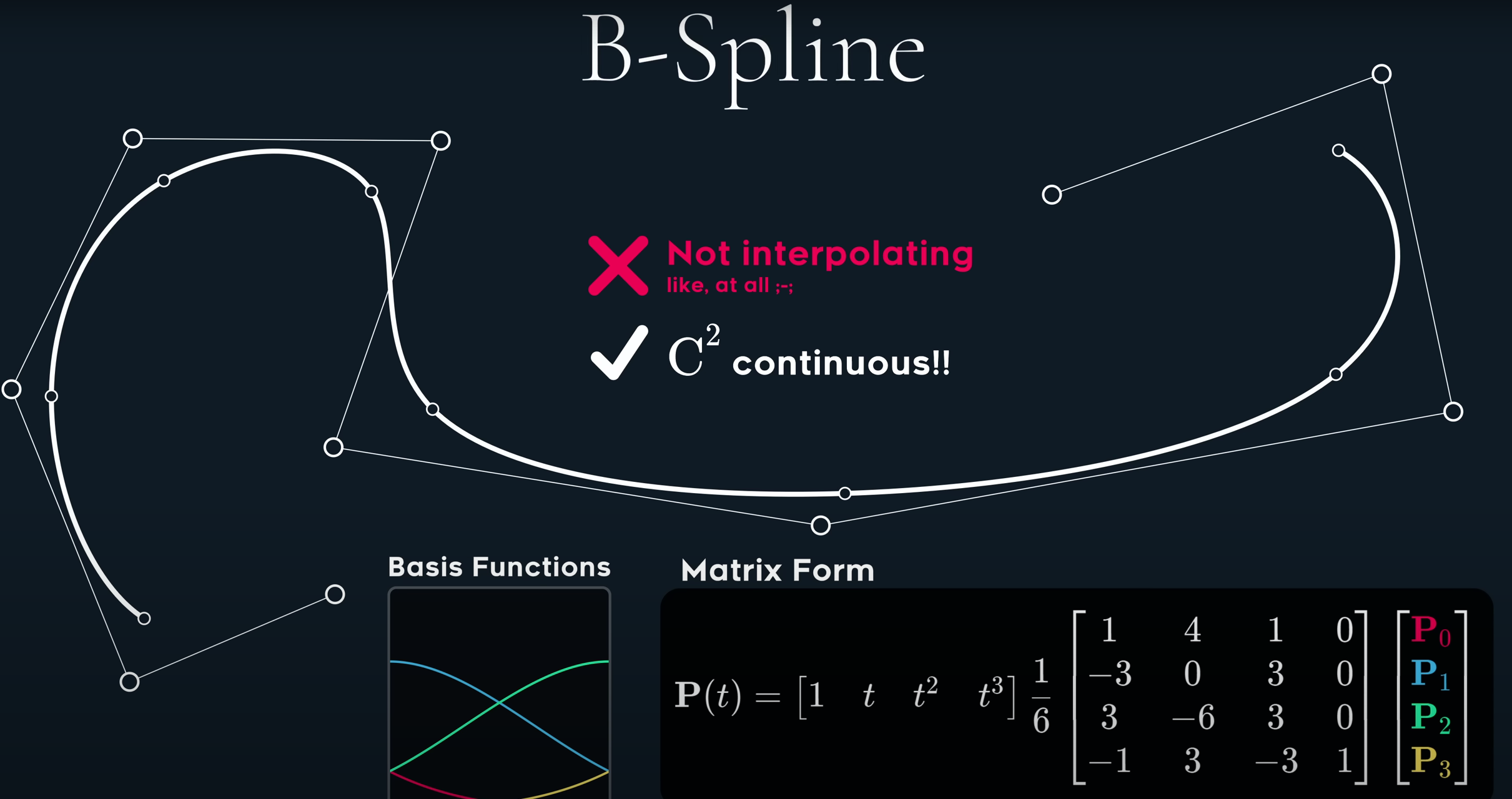
B-Splines
nurbs曲线
未完待续……
Q.E.D.