图片链接在github上面,如果不能查看图片,请检查网络状态
前言
在计算机图形学领域,有着许许多多的分支,有些随着游戏进入公众的视野,有些随着AI的进步广泛的收到关注。但是还有一些细分领域,其重要程度不亚于以上两方面,却相对较为冷清。它就是三维建模。
三维建模被广泛的应用于工业领域和视频领域。可以说,三维建模技术支撑起了当今的现代制造业。相比于游戏建模,工业领域的三维建模对于几何数据的约束和拓扑结构的组织更为严格,为了实际生产出于设计指标相同的产品,工业软件的三维建模往往要求每一个点、线、面都要保留几何拓扑信息,以便于随时进行形体的计算与修改。而组织、表达三维形体的方式,就是组成三维建模技术的基石。
常见的三维形体表达方式
常见的三维形体表达方式,大致可以利用控制形体表达元素维度来进行区分。常见的表达方式有点云表达、边界表达、体素表达。其中,点云表达常常出现在一些较为特殊的使用场景中,对于一些传统的工业领域,边界表达(B-Rep)与体素表达(CSG)仍然是主力的表达方式。我们今天将着重介绍边界表达的三维建模方式。
当前工业软件的内核情况概述
作为一款工业设计软件,无论是CAD、CAM亦或是EDA,核心的建模能力都体现在模型的快速构建、修改、展示、保存上,也就是如何规范化、结构化三维数据,并提供接口修改该结构。这是一个需要顶层设计和后续修补的庞大系统,结合上各行各业的工业需求,市场上也诞生了不少优秀的工业软件建模内核。
我们简单的举个例子,达索公司旗下的CATIA、SoildWorks;西门子旗下的UG,他们使用的内核有ACIS、Parasolid、CGM等等,但是在功能设计上都为了满足高效的几何约束求解、几何建模等任务。在某些结构设计上也大同小异。
我们今天将借鉴达索公司CATIA V5中对三维建模的表达完成下面文章的表述。对于基础的曲线曲面知识,文章中不会提及,希望更进一步的同学,请自己下载CATIA二次开发系统进行调试和开发。公司官网我给放这里 https://www.3ds.com/zh-hans/
对于一些熟悉CAA二次开发的朋友,出于尊重各家版权以及便于理解的原因,这篇文章中一些特征与名词,可能会被我稍加修改,请理解。
B-Rep表达的组织结构
言归正传,我们回归三维数据本身,在建模中,我们需要明确的输入形体的位置信息(点与面在哪里),输入形体的形状(点线面之间怎么相连)。这两个部分的信息我们分别叫做几何信息、拓扑信息。拥有了几何与拓扑,一个完整的三维形体就可以被构建出来。站在计算机的角度,就是要将这两大类的信息,结构化之后,塞到内存和硬盘中。
当然,如何进行软件架构,是计算机工程人员需要考虑的事情。我们先着眼于如何结构化这两大类数据。
几何数据
先从几何数据说起,已知我们的世界是三维的,三维物体应当由二维元素连接填充构成。二维平面则由一维线段构成,一维直线由零维的点组成。
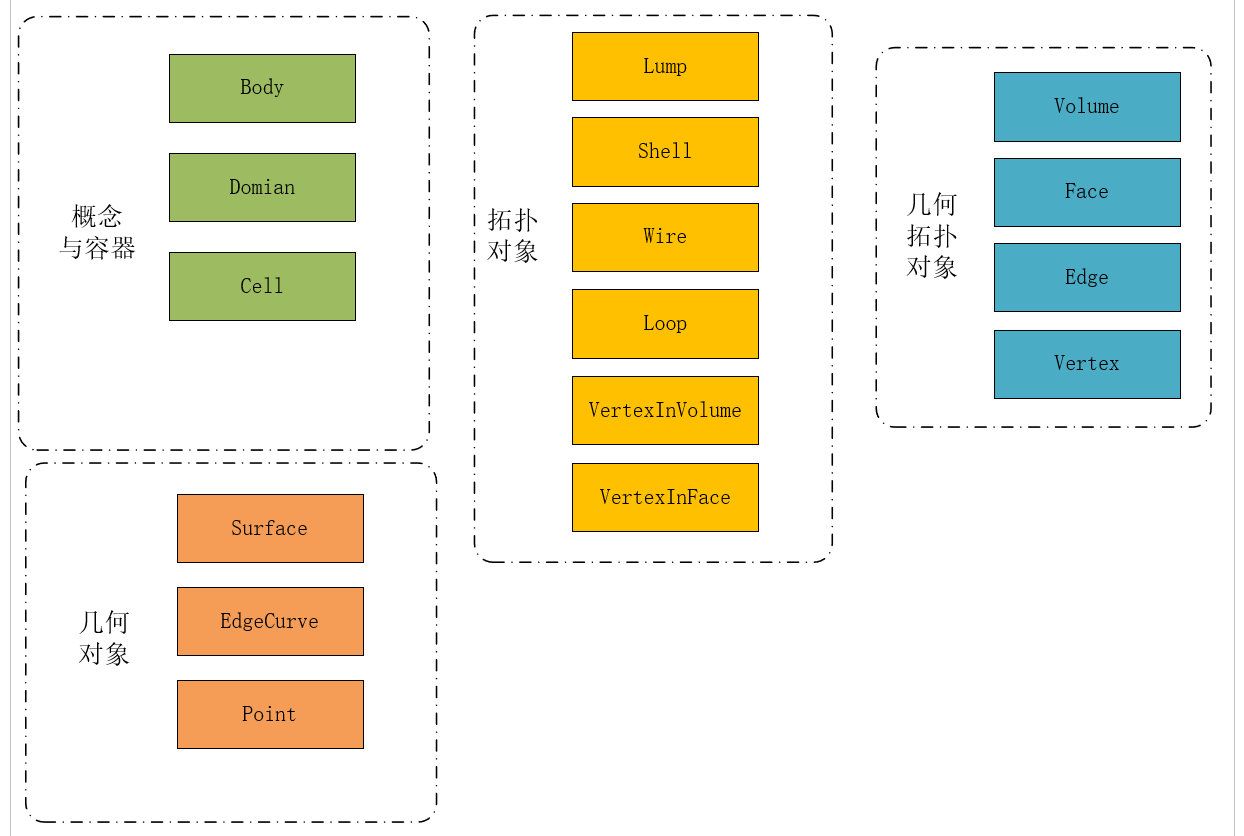
也就是说,在几何数据部分,我们至少,应当有四个抽象的数据结构,在C++里,也就是四个类定义。在CATIA V5中,这四个类分别为Volume(包络体) 、Surface(曲面)、EdgeCurve(边界)、Point(顶点)
顶点就是空间中的一个点,它存有自己的三维坐标,是最基本的集合元素。
边界是约束曲面形状的几何元素,它本质是一条或多条相连曲线,也继承了曲线应有的数据结构。和所有的线一样,它只有一个自由度,也就是沿着曲线向前或者向后,但是它本身可以是二维、甚至三维的元素,这取决于它的几何特性。它应当含有至少两个顶点,即开始与结束点,并且,由于不同的表达方式和连接手段,含有不同的控制数据。例如使用nurbs表达的曲线将会有控制点、节点向量等用来描述曲线的必要信息。
曲面是用于约束三维形体的几何元素,在一些情况下,它由空间中的闭合曲线填充得来,也就是说,曲面拥有闭合的曲线边界。所以,它至少应该有一个能存储边界的容器,除此之外,构建曲面的过程与构建曲线相似,使用不同方式构建的曲面将含有不同的控制元素。除此之外,我们将会在建模中遇到一些特殊的情况,比如曲面的某一点突然维度跌落,这样非流行的曲面告诉我们,高维度的几何类应当可以留有容器用于存储所有低于它维度的几何信息。
包络体是用于表达三维形体的几何元素,它可以容纳以上任何元素。需要注意的是,在CATIA中,CATVolume几乎已经被废弃,我们这里保留它是希望几何结构保持完整。个人认为其原定的功能已经被CATBody接管,在开发中几乎不会遇到CATVolume这个类,至于具体的原因,我们不去深究。
拓扑数据
几何数据仅仅约束了单一的元素的形状,如果只是对单一的模型进行展示,好像也不需要拓扑数据的参与。但是在实际的工作环境中,往往是多个模型共享一个工作域,并且模型形体随时可能调整,模型之间也需要进行布尔运算等操作。此时就不得不需要原始模型的拓扑输出参与了。
拓扑数据记录的是元素与元素之间的关系,在上文中,我们定义了四种几何元素,是不是就意味着需要6中拓扑关系呢?其实也不尽然,我们还是要根据实际的需求出发来定义拓扑结构数据。
在CATIA中,拓扑结构有六类:Lump(块)Shell(壳)Wire(线框)Loop(环)VertexInVolume(包络体点)VertexInFace(曲面点)
每一类拓扑结构都描述了一种几何组成的关系。
Lump描述的是体,即三维的拓扑结构。它涵盖了表示面与体、点与体的拓扑关系。
shell表述的是面,它也是一种三维的拓扑结构,但是自由度降为二维。它包含面与面之间的拓扑关系
wire表述的是线框,同样,它存在于三维空间中,但自由度为一维。它描述的是线与线之间的关系。
loop表述的是环,它是一种辅助的拓扑描述结构,因为在一个面中,可能会有多个封闭的边界,并且他们分为内边界和外边界。环的出现可以帮助我们分辨当前的内外边界等信息。
VertexInVolume与VertexInFace,他们代表点的拓扑关系,分别是在体上的点和在面上的点。因为在实际的模型中,可能会出现非流行的模型,对于这种维度突然跌落到零维的情况,这两种点拓扑关系的描述就派上了用场。
依据上面的描述,我们使用更加直观清晰的图解来描述是上述结构:
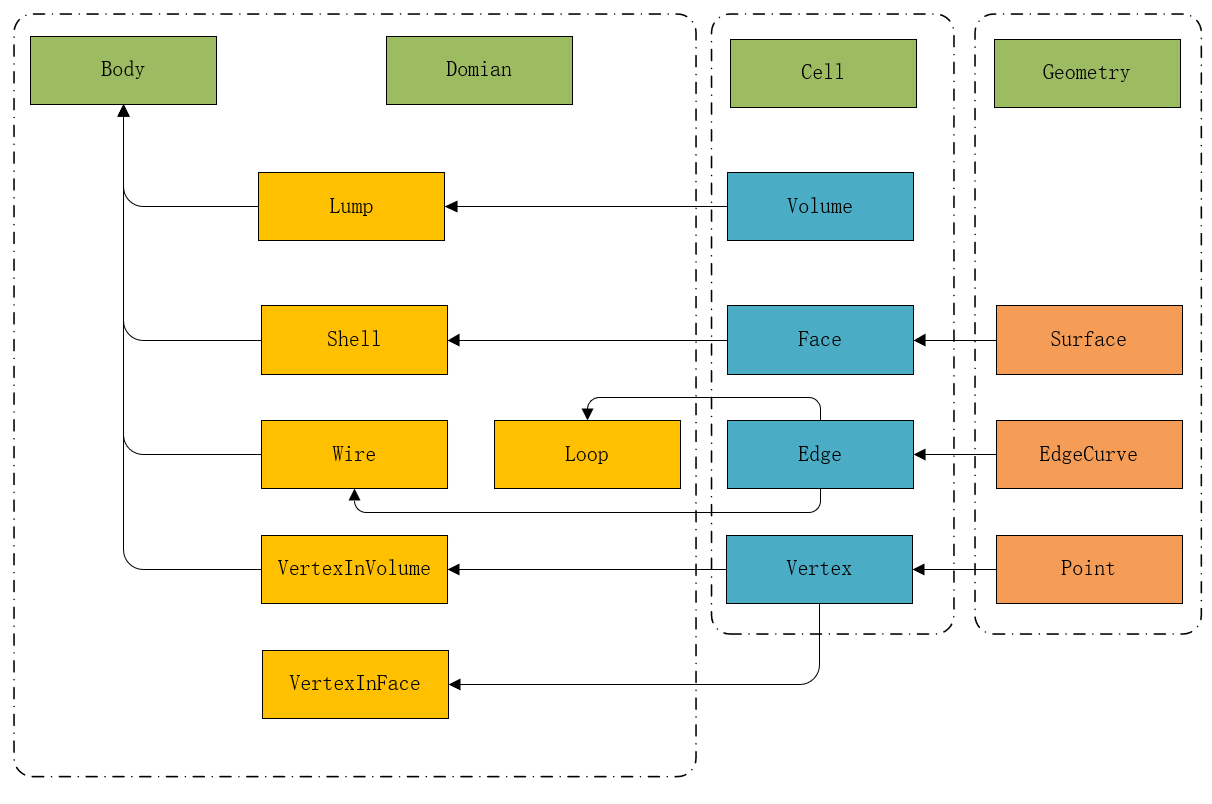
Q.E.D.








