四元数与3D旋转
前言
-所有的图片挂载于github,若不能查看,请检查网络状态
-文章仅涉及简单的四元数定义与其在几何中的应用,不涉及群论等数学内容(因为我也不会)
四元数简介
四元数,或者我们称其为汉密尔顿四元数,从数学意义上讲,是对于复数集合的一次扩充。它引入了更多的复数维度,用于描述更为复杂的空间操作。
四元数的发明起源与数学家们期望寻找“三维复数”,我们知道二维空间中,将一个轴定义为虚轴就可以建立二维复数的表示坐标系。当然,我们也可以将虚数轴暂时隔离出来,我们就会得到一个实数轴(一维空间)和一个二维变量(复数)。记住这个模型,在后面它将作为intro引入四元数的物理意义。
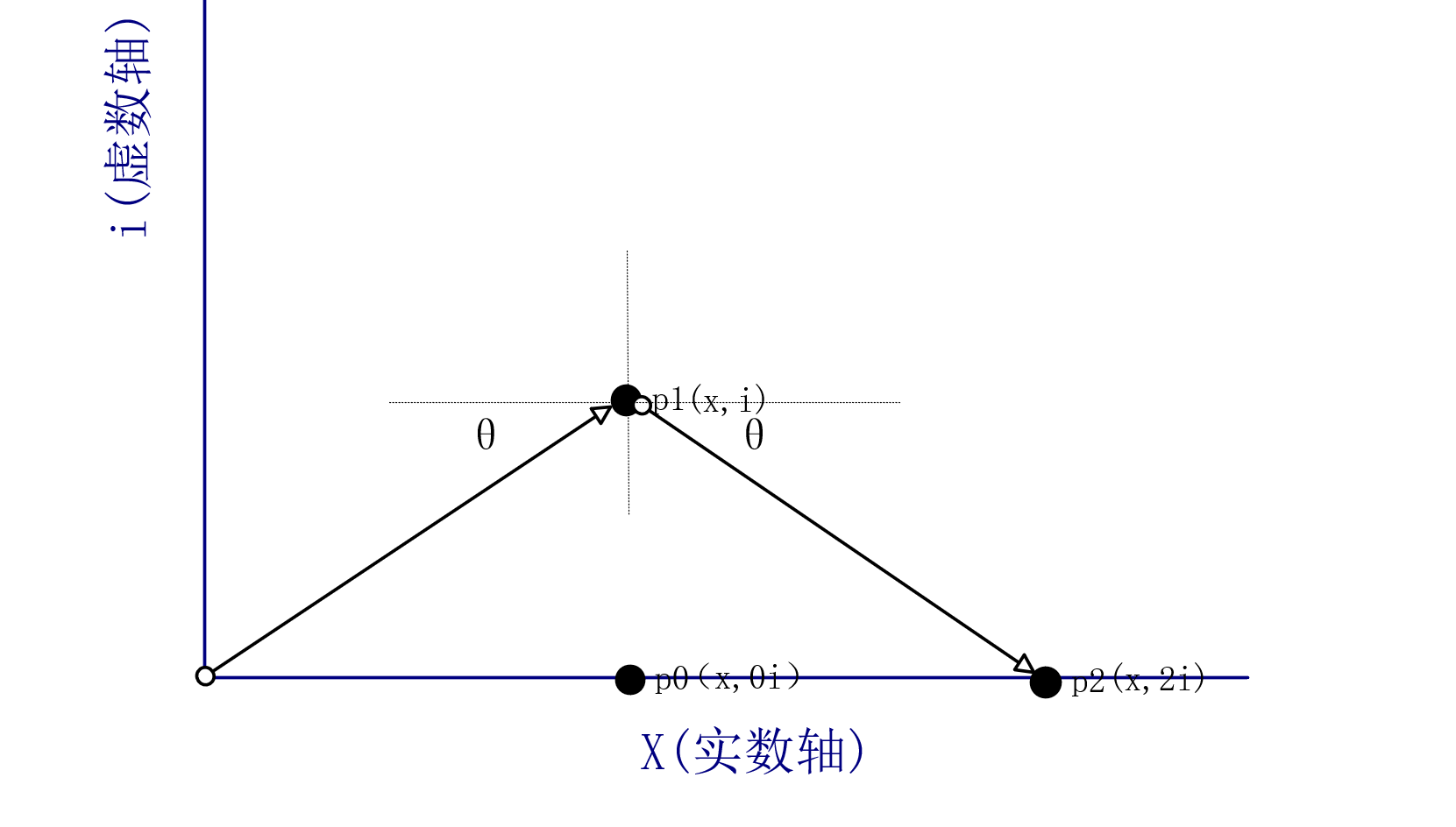
按照我们小学二年级的知识,坐标轴有几条就会代表这是几维的空间,那么,只需要添加一个虚轴(一个实轴,两个虚轴)就可以组成三维的空间。但是事实告诉我们,使用这种方式,无法正常的描述和计算三维空间中的变化。很多数学家都卡在了这一步,笔者理解的原因是因为复数(i)的性质导致其能表示的范围收窄了。我们可以粗略的将复数理解为实数的投影,也就是利用一个单位球进行映射:
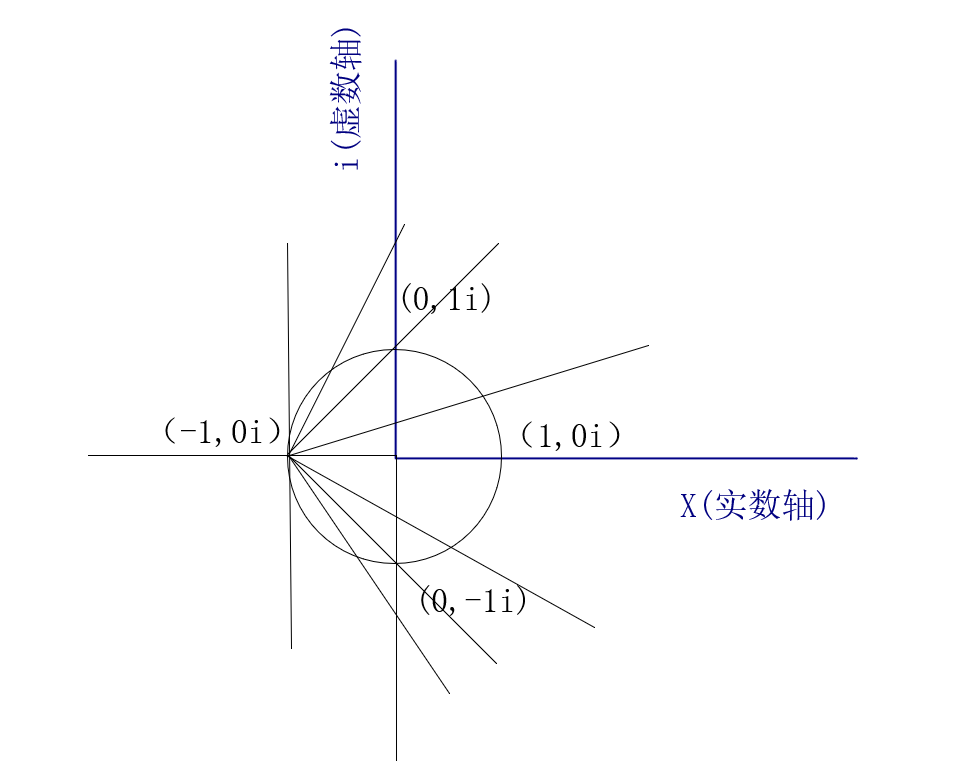
不难看出,实数与虚数是有关系的,但是并不是简单的线性关系,所以想要单纯使用两个虚数代替两个实数构建坐标,是不利于计算和定义的(事实上我们也办不到)。那能不能增加更多的虚数来进行描述呢,很遗憾,你并不能证明,使用虚轴的坐标系在其物理性质上可以等同于实数坐标系。但是汉密尔顿想解决的问题,仅仅是使用复数描述空间变换,而不是空间本身,所以,增加虚数的作用,就变成了使用高维变换作用于低维空间,这就要引出我们接下来要讨论的内容:四维空间变换与三维空间。
同时,我们先抛出四元数的计算公式,并希望大家先行思考,为什么公式长成这个样子,在不进行任何数学推导的情况下,它是否满足我们对数学公式的最高评价:符合直觉。
虚数轴定义:
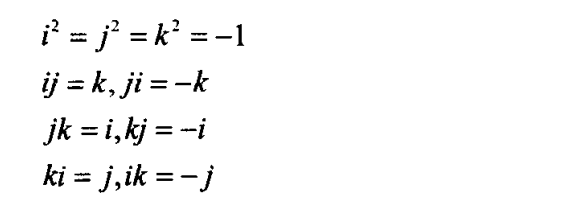
四元数定义:
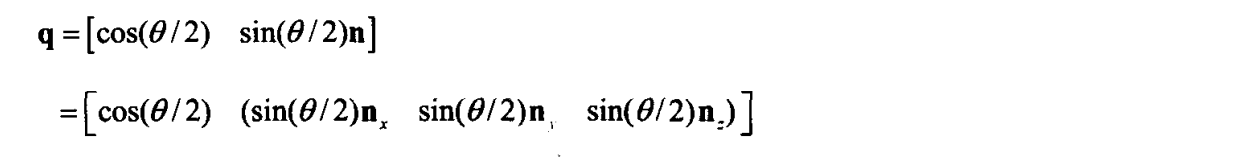
四元数表达点旋转:
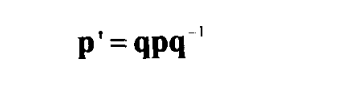
三维空间的旋转表示
对计算机图形学有所了解的同学应该对三维空间变换如数家珍,旋转作为最为常见的空间变换,已经刻进了他们的DNA里面。我相信大部分人对于旋转的最初理解都源自于旋转矩阵,旋转矩阵是一个很优秀的方式来表述旋转,它等同于坐标系的线性变换,同时也利于进行连续变换的计算。所以,我们将会以旋转矩阵为中心介绍其他的三维旋转的原理。
首先我们介绍一下旋转矩阵,众所周知,三阶矩阵可以用来表述一个三维点坐标(三个向量从原点开始的平移|单个向量也可以表达一个三维点)。而如果先找出一个旋转轴,那么就只需要两个变量就可以完成旋转,现在我们先设定一个点V,一个旋转轴n,一个旋转角度θ。旋转表达如下:
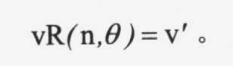
现在,我们试着求解R(旋转矩阵),我们只贴出一个向量的求解方式:

三维旋转的矩阵表达我们先说到这里,重点是四元数的物理理解
四元数旋转原理
在初步了解了三维旋转的表示方法之后,我们不难发现,只有四元数是无法直观理解的,这是因为我们习惯了三维空间的表述,对于更高维度的空间无法想象。所以,我们需要使用归纳与推理的方式,尝试从低维到高维理解四元数。
首先,我们返回第一张图:,我们认为其原有的空间为一维空间,在一维空间上的点是x(),他可以表示一个一维向量。
现在,我们在加入i轴之后,取平面上一个点p,连接原点与p点,构成一个二维向量。
使用二维向量左乘这个一维向量,可以得到一个新的向量,其指向的点为p2。
此时我们发现,p2已经不在原有的一维坐标系上,而是“升维”到了二维平面上。也就是说,在经过了更高维度的变换之后,空间中的点脱离了原本的坐标系空间。
我们自然是不希望一次变换之后,整个世界中都缺失了变换点,所以我们需要把这个点重新变换回原有的坐标系。既然高位变换可以升维,那么其逆向变换,或者说反方向变换应该也可以降维。
我们在原有的空间中找到一个p3,连接p2p3,使用向量v2就可以使得目标点重新变换到原有的坐标系中。至于为什么要选p3,是因为,从向量的角度出发,我们只需要把已知的向量同角度反向旋转,就可以完成操作,无需引入其他变量。

在明白上述的过程之后,我们试着将它扩展到三维空间中。
三维空间中体的旋转可以代替为所有顶点的旋转,而点的旋转可以代替为点的位移。所以,我们先求解一个点的旋转位移。
我们在使用旋转矩阵进行变换时,可以直观地理解为点不动,矩阵乘法会导致坐标系的变换,从而反映到点的坐标上。
但是四维的旋转难以想象,依据我们之前的推导,一次左乘就能将三维坐标中的点转移到四维空间中。而这种向量乘法可以通过“反方向”的方法,也就是向量逆的右乘使得坐标重新回归原有空间。这也是为什么我们要取角度的二分之一,进行两次乘法。
同样,你可以在其他文章中找到四维空间“左旋、右旋”的表述,这里我们不再解释。
四元数与矩阵、欧拉角的转换
三种表达方式一共有九种变化,但是我们常用的一般为三种。矩阵->四元数;四元数->矩阵;欧拉角->四元数。
其中,矩阵承担了计算和中转的职责,四元数的优势在于插值和计算,欧拉角则更多的是提供给用户侧进行输入所使用的。
这几种表达方式的优劣我们借用书中的一个表格展示:

参考资料
部分图片:《3D数学基础:图形与游戏开发》
Q.E.D.








